
 loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围.
loga2x+loga2y=loga(ax2)+loga(ay2)(a>0且a≠1),求loga(xy)的取值范围. 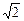 ,最小值为1+
,最小值为1+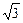 ;
;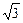 ,最小值为2-2
,最小值为2-2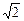 .
. loga2x+loga2y=(1+2logax)+(1+2logay),
loga2x+loga2y=(1+2logax)+(1+2logay),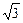 ≤k≤2(1+
≤k≤2(1+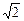 );
);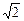 )≤k≤1-
)≤k≤1-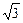 .
. 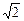 ,最小值为1+
,最小值为1+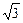 ;
;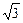 ,最小值为2-2
,最小值为2-2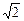 .
. 

科目:高中数学 来源:不详 题型:解答题
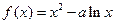 在区间[1,2]上是增函数,且
在区间[1,2]上是增函数,且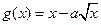 在区间[0,1]上是减函数。
在区间[0,1]上是减函数。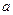 的值;
的值;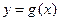 图象上任意一点,求点P到直线
图象上任意一点,求点P到直线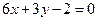 距离的最小值;
距离的最小值; 且
且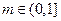 时,
时,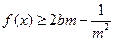 恒成立,求
恒成立,求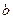 的取值范围。
的取值范围。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
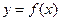 的反函数为
的反函数为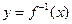 ,定义:若对给定的实数
,定义:若对给定的实数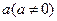 ,函数
,函数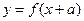 与
与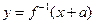 互为反函数,则称
互为反函数,则称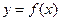 满足“
满足“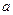 和性质”.
和性质”.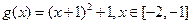 是否满足“1和性质”,并说明理由;
是否满足“1和性质”,并说明理由; 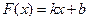 ,其中
,其中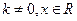 满足“2和性质”,则是否存在实数a,使得
满足“2和性质”,则是否存在实数a,使得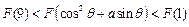 对任意的
对任意的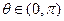 恒成立?若存在,求出
恒成立?若存在,求出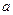 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
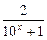 -1(x∈R)的反函数,函数g(x)的图像
-1(x∈R)的反函数,函数g(x)的图像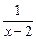 的图像关于y轴对称,设F(x)=f(x)+g(x).
的图像关于y轴对称,设F(x)=f(x)+g(x). 
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.正数 | B.负数 | C.非负数 | D.正数、负数和零都有可能 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
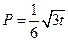 ,
,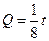 .今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).
.今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 亩产量(单位:千克) | 300 | 320 | 330 | 340 |
| 亩数 | 20 | 25 | 40 | 15 |
| 亩产量(单位:千克) | 310 | 320 | 330 | 340 |
| 亩数 | 30 | 20 | 40 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com