
【题目】已知函数f(x)=x2-2(a+1)x+2alnx
(1)若a=2. 求f(x)的极值. (2)若a>0. 求f(x)的单调区间.
【答案】(1)![]() ,
, ![]() .(2)详见解析.
.(2)详见解析.
【解析】试题分析:先求解(2):定义域为![]() ,对函数求导得
,对函数求导得![]() ,由于
,由于![]() ,故分为
,故分为![]() 三类,讨论函数的单调区间.(1)由前面的分析可知,当
三类,讨论函数的单调区间.(1)由前面的分析可知,当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ,故极小值为
,故极小值为![]() ,极大值为
,极大值为![]() .
.
试题解析:由题知, x>0, ![]() ,
,
令f′(x)=0得x1=a,x2=1, 当0<a<1时,在x∈(0,a)或x∈(1,+∞)时,f′(x)>0,
在x∈(a,1)时,f′(x)<0,
所以f(x)的单调递增区间为(0,a)和(1,+∞),单调递减区间为(a,1);当a=1时, ![]() ,
,
所以f(x)的单调递增区间为(0,+∞); 当a>1时,在x∈(0,1)或x∈(a,+∞)时,f′(x)>0,在x∈(1,a)时,f′(x)<0,
所以f(x)的单调递增区间为(0,1)和(a,+∞),单调递减区间为(1,a).
(1)当a=2时,在x∈(0,1)或x∈(2,+∞)时,f′(x)>0,在x∈(1,2)时,f′(x)<0,
所以x=1时有极大值: ![]()
所以x=2时有极大值: ![]()
(2)综上:当0<a<1时,f(x)的单调递增区间为(0,a)和(1,+∞),单调递减区间为(a,1);
当a=1时,f(x)的单调递增区间为(0,+∞);
当a>1时,f(x)的单调递增区间为(0,1)和(a,+∞),单调递减区间为(1,a).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4, ![]() ,AB=2CD=8.
,AB=2CD=8.
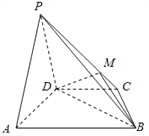
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)在(2)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得以
,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() 的交点,若存在,求出点
的交点,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]()
(1)求函数![]() 的单调递减区间;
的单调递减区间;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不等的根,求实数
上有两个不等的根,求实数![]() 的取值范围;
的取值范围;
(3)若存在![]() ,当
,当![]() 时,恒有
时,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数,
为常数, ![]() 是自然对数的底数),曲线
是自然对数的底数),曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() .
.
(1)求![]() 的值;(2)求
的值;(2)求![]() 的单调区间;
的单调区间;
(3)设![]() (其中
(其中![]() 为
为![]() 的导函数)。证明:对任意
的导函数)。证明:对任意![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学参加科普知识竞赛,需回答3个问题,竞赛规则规定:答对第一、二、三问题分别得100分、100分、200分,答错得零分,假设这名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6,且各题答对与否相互之间没有影响.
(1)求这名同学得300分的概率;
(2)求这名同学至少得300分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com