
【题目】某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本C(x),当年产量不足80千件时,C(x)= ![]() x2+10x(万元);当年产量不小于80千件时C(x)=51x+
x2+10x(万元);当年产量不小于80千件时C(x)=51x+ ![]() ﹣1450(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
﹣1450(万元),通过市场分析,若每件售价为500元时,该厂本年内生产该商品能全部销售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获的利润最大?
【答案】
(1)解:∵每件商品售价为0.05万元,
∴x千件商品销售额为0.05×1000x万元,
①当0<x<80时,根据年利润=销售收入﹣成本,
∴L(x)=(0.05×1000x)﹣ ![]() ﹣10x﹣250=﹣
﹣10x﹣250=﹣ ![]() +40x﹣250;
+40x﹣250;
②当x≥80时,根据年利润=销售收入﹣成本,
∴L(x)=(0.05×1000x)﹣51x﹣ ![]() +1450﹣250=1200﹣(x+
+1450﹣250=1200﹣(x+ ![]() ).
).
综合①②可得,L(x)= 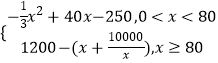
(2)解:①当0<x<80时,L(x)=﹣ ![]() +40x﹣250=﹣
+40x﹣250=﹣ ![]() +950,
+950,
∴当x=60时,L(x)取得最大值L(60)=950万元;
②当x≥80时,L(x)=1200﹣(x+ ![]() )≤1200﹣2
)≤1200﹣2 ![]() =1200﹣200=1000,
=1200﹣200=1000,
当且仅当x= ![]() ,即x=100时,L(x)取得最大值L(100)=1000万元.
,即x=100时,L(x)取得最大值L(100)=1000万元.
综合①②,由于950<1000,
∴年产量为100千件时,该厂在这一商品的生产中所获利润最大
【解析】(1)分两种情况进行研究,当0<x<80时,投入成本为C(x)=) ![]() +10x(万元),根据年利润=销售收入﹣成本,列出函数关系式,当x≥80时,投入成本为C(x)=51x+
+10x(万元),根据年利润=销售收入﹣成本,列出函数关系式,当x≥80时,投入成本为C(x)=51x+ ![]() ﹣1450,根据年利润=销售收入﹣成本,列出函数关系式,最后写成分段函数的形式,从而得到答案;(2)根据年利润的解析式,分段研究函数的最值,当0<x<80时,利用二次函数求最值,当x≥80时,利用基本不等式求最值,最后比较两个最值,即可得到答案.
﹣1450,根据年利润=销售收入﹣成本,列出函数关系式,最后写成分段函数的形式,从而得到答案;(2)根据年利润的解析式,分段研究函数的最值,当0<x<80时,利用二次函数求最值,当x≥80时,利用基本不等式求最值,最后比较两个最值,即可得到答案.


科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,点A的极坐标为(3, ![]() ),点B的极坐标为(6,
),点B的极坐标为(6, ![]() ),曲线C:(x﹣1)2+y2=1
),曲线C:(x﹣1)2+y2=1
(1)求曲线C和直线AB的极坐标方程;
(2)过点O的射线l交曲线C于M点,交直线AB于N点,若|OM||ON|=2,求射线l所在直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位: ![]() ).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布
).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记![]() 表示一天内抽取的16个零件中其尺寸在
表示一天内抽取的16个零件中其尺寸在![]() 之外的零件数,求
之外的零件数,求![]() 及
及![]() 的数学期望;
的数学期望;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
(ⅰ)试说明上述监控生产过程方法的合理性;
(ⅱ)下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得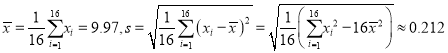 ,其中
,其中![]() 为
为
抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是空间两条直线,
是空间两条直线, ![]() 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )
A. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
D. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
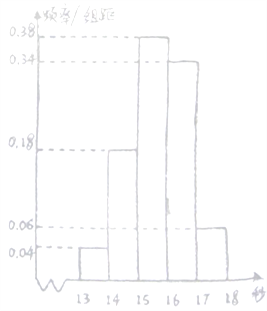
(1)请根据频率分布直方图估计该组数据的众数和中位数(精确到0.1);
(2)从成绩介于![]() 和
和![]() 两组的人中任取2人,求两人分布来自不同组的概率.
两组的人中任取2人,求两人分布来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}满足a1=1,且a1 , a2 , a5成等比数列.
(1)求{an}的通项公式;
(2)若bn=(﹣1)n ![]() (n∈N*),求数列{bn}的前n项和Sn .
(n∈N*),求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)若AB⊥AC,AB=AC=1,AA1=2,求几何体ABD-A1B1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一辆赛车在一个周长为![]() 的封闭跑道上行驶,跑道由几段直道和弯道组成,图
的封闭跑道上行驶,跑道由几段直道和弯道组成,图![]() 反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.
反映了赛车在“计时赛”整个第二圈的行驶速度与行驶路程之间的关系.

图1

图2
根据图![]() 有以下四个说法:
有以下四个说法:
①在这第二圈的![]() 到
到![]() 之间,赛车速度逐渐增加;
之间,赛车速度逐渐增加;
②在整个跑道中,最长的直线路程不超过![]() ;
;
③大约在这第二圈的![]() 到
到![]() 之间,赛车开始了那段最长直线路程的行驶;
之间,赛车开始了那段最长直线路程的行驶;
④在图![]() 的四条曲线(注:
的四条曲线(注:![]() 为初始记录数据位置)中,曲线
为初始记录数据位置)中,曲线![]() 最能符合赛车的运动轨迹.
最能符合赛车的运动轨迹.
其中,所有正确说法的序号是( )
A. ①②③ B. ②③ C. ①④ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com