
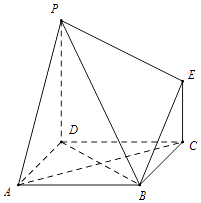
【题目】如图为一组合几何体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD且PD=AD=2EC=2.
(I)求证:AC⊥平面PDB;
(II)求四棱锥B﹣CEPD的体积;
(III)求该组合体的表面积.
【答案】(Ⅰ)证明:∵PD⊥平面ABCD,∴PD⊥AC,又底面ABCD为正方形,∴AC⊥BD,
∵BD∩PD=D,
∴AC⊥平面PDB;
(Ⅱ)解:∵PD⊥平面ABCD,且PD面PDCE,
∴面PDCE⊥面ABCD,又BC⊥CD,∴BC⊥平面PDCE.
∵S梯形PDCE= ![]() (PD+EC)DC=
(PD+EC)DC= ![]() ×3×2=3,
×3×2=3,
∴四棱锥B﹣CEPD的体积VB﹣CEPD= ![]() S梯形PDCEBC=
S梯形PDCEBC= ![]() ×3×2=2;
×3×2=2;
(Ⅲ)解:∵BE=PE= ![]() ,PB=2
,PB=2 ![]() ,
,
∴SPBE= ![]() ×2
×2 ![]() ×
× ![]() =
= ![]() .
.
又∵SABCD=2×2=4,SPDCE=3,SPDA= ![]() =2,SBCE=
=2,SBCE= ![]() =1,SPAB=
=1,SPAB= ![]() =2
=2 ![]() ,
,
∴组合体的表面积为10+2 ![]() +
+ ![]() .
.
【解析】(Ⅰ)由已知结合线面垂直的性质可得PD⊥AC,又底面ABCD为正方形,得AC⊥BD,再由线面垂直的判定得AC⊥平面PDB;(Ⅱ)由PD⊥平面ABCD,可得面PDCE⊥面ABCD,进一步得到BC⊥平面PDCE.求出S梯形PDCE , 代入棱锥体积公式求得四棱锥B﹣CEPD的体积;(Ⅲ)求解直角三角形得△PBE的三边长,再由三角形面积公式可得组合体的表面积.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】设函数f(x)= 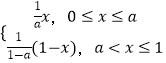 ,a为常数,且a∈(0,1).
,a为常数,且a∈(0,1).
(1)若x0满足f(x0)=x0 , 则称x0为f(x)的一阶周期点,证明函数f(x)有且只有两个一阶周期点;
(2)若x0满足f(f(x0))=x0 , 且f(x0)≠x0 , 则称x0为f(x)的二阶周期点,当a= ![]() 时,求函数f(x)的二阶周期点.
时,求函数f(x)的二阶周期点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinx﹣bcosx(a、b为常数,a≠0,x∈R)在x= ![]() 处取得最小值,则函数y=f(
处取得最小值,则函数y=f( ![]() ﹣x)是( )
﹣x)是( )
A.偶函数且它的图象关于点(π,0)对称
B.偶函数且它的图象关于点 ![]() 对称
对称
C.奇函数且它的图象关于点 ![]() 对称
对称
D.奇函数且它的图象关于点(π,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形.
(Ⅰ)求二面角P﹣AB﹣C的大小;
(Ⅱ)在线段AB上是否存在一点E,使平面PCE⊥平面PCD?若存在,请指出点E的位置并证明,若不存在请说明理由.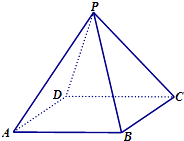
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)求函数f(x)的单调区间;
(3)若函数 ![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(ex﹣1)(x﹣1)k , k∈N* , 若函数y=f(x)在x=1处取到极小值,则k的最小值为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com