
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 是正方形,
是正方形,![]() 是正三角形,
是正三角形,![]() ,
, ![]() ,
,![]() .
.
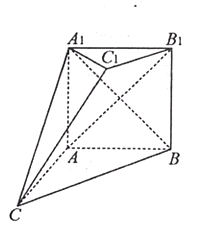
(1)求证:![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,过点M(1,0)的直线l与抛物线C:y2=2px(p>0)交于A,B两点,且![]() .
.
(1)求抛物线C的方程;
(2)过点M作直线l'⊥l交抛物线C于两点,记△OAB,△OPQ的面积分别为S1,S2,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”.他把三角形的三条边分别称为小斜、中斜和大斜.三斜求积术就是用小斜平方加上大斜平方,送到中斜平方,取相减后余数的一半,自乘而得一个数,小斜平方乘以大斜平方,送到上面得到的那个数,相减后余数被4除,所得的数作为“实”,1作为“隅”,开平方后即得面积.所谓“实”、“隅”指的是在方程![]() 中,p为“隅”,q为“实”.即若
中,p为“隅”,q为“实”.即若![]() 的大斜、中斜、小斜分别为a,b,c,则
的大斜、中斜、小斜分别为a,b,c,则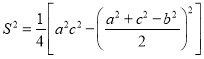 .已知点D是
.已知点D是![]() 边AB上一点,
边AB上一点,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积为________.
的面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com