
分析 (Ⅰ)首先化简两个命题,明确几何测度为区间长度,利用区间长度的比求概率;
(Ⅱ)由(1)d结论得到所有基本事件数,利用古典概型公式求解.
解答 解:(Ⅰ)P:x∈R且x2+2x-3<0,即x∈(-3,1);Q:x∈R且$\frac{x+2}{x-3}$<0.即(-2,3)
在区间(-4,4)上任取一个实数x,对应区间长度为8,命题“P且Q”为真的x范围为(-2,1),区间长度为3,所以命题“P且Q”为真的概率$\frac{3}{8}$.
(Ⅱ)在(Ⅰ)的基础上易知,a=-2,-1,0,b=-1,0,1,2,则基本事件(a,b)共有12个:(-2,-1),(-2,0),(-2,1),(-2,2),(-1,-1),(-1,0),(-1,1),(-1,2),(0,-1),(0,0),(0,1),(0,2).
“P或Q”真?P真或Q真?-3<x<3,符合事件b-a∈{x|P或Q真}”的基本事件为:(-2,-1),(-2,0),(-1,-1),(-1,0),(-11),(0,-1),(0,0),(0,1),(0,2),共9个.
故事件“事件b-a∈{x|P或Q真}”发生的概率$\frac{9}{12}=\frac{3}{4}$. …(12分)
点评 本题考查了几何概型和古典概型的概率求法;关键是明确概率模型,采用正确的公式求解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{15}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若t<-2,g(x)有四个零点 | B. | 若t=-2,g(x)有三个零点 | ||
| C. | 若-2<t<$\frac{1}{4}$,g(x)有两个零点 | D. | 若t=$\frac{1}{4}$,g(x)有一个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
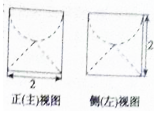 若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )
若某圆柱体的上部挖掉一个半球,下部挖掉一个圆锥后所得的几何体的三视图中的正(主)视图和侧(左)视图如图所示,则此几何体的表面积是( )| A. | (4+$\sqrt{2}$)π | B. | 6$π+2\sqrt{2}π$ | C. | 6$π+\sqrt{2}π$ | D. | (8+$\sqrt{2}$)π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com