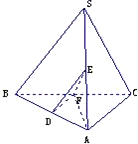
解:(1)∵∠SAB=∠SAC=∠ACB=90°,∴SA⊥面BAC,即SA即是棱锥的高,
又AC=1,BC=

,SB=2

,=∠ACB=90°
∴AB=2,SA=2

∴三角形BAC的面积为
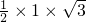
=

,三棱锥S-ABC的体积为
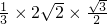
=

(2)由(1)知SA⊥面BAC可得SA⊥BC
又=∠ACB=90°,可得BC⊥AC,又SA∩AC=A
∴BC⊥面SCA
∴BC⊥SC
(3)分别取AB、SA、BC的中点D、E、F,连接ED、DF、EF、AF,由于ED∥SB,DF∥AC,故∠EDF(或其邻补角)就是异面直线SB和AC所成的角
由上证知DE=

SB=

,DF=

AC=

,AE=

,在直角三角形ACF中可求得AF=

在直角三角形EAF中可求得EF=
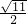
在三角形DEF中由余弦定理得∠EDF余弦的绝对值为
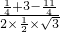
=

分析:(1)求三棱锥S-ABC的体积,由题设条件得,棱锥的高是SA,底面是直角三角形,体积易求;
(2)证明BC⊥SC可通过证明BC⊥面ASC来证;
(3)分别取AB、SA、BC的中点D、E、F,连接ED、DF、EF、AF,可得∠EDF(或其邻补角)就是异面直线SB和AC所成的角
点评:本题考查求异面直线所成的角,求解本问题的关键是注意到所得出的角不一定就两异面直线的夹角有可能是夹角的补角.

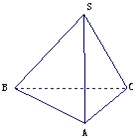 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC= ,SB=2
,SB=2 .
. 解:(1)∵∠SAB=∠SAC=∠ACB=90°,∴SA⊥面BAC,即SA即是棱锥的高,
解:(1)∵∠SAB=∠SAC=∠ACB=90°,∴SA⊥面BAC,即SA即是棱锥的高, ,SB=2
,SB=2 ,=∠ACB=90°
,=∠ACB=90°
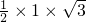 =
= ,三棱锥S-ABC的体积为
,三棱锥S-ABC的体积为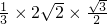 =
=
 SB=
SB= ,DF=
,DF= AC=
AC= ,AE=
,AE= ,在直角三角形ACF中可求得AF=
,在直角三角形ACF中可求得AF=
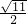
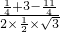 =
=


 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.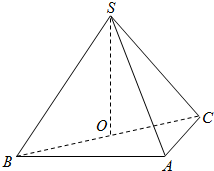 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,AC=2 C.
C. 如图,在三棱锥S-ABC中,SA=AB=BC=AC=
如图,在三棱锥S-ABC中,SA=AB=BC=AC=