练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，天花板上挂着3串玻璃球，射击玻璃球规则：每次击中1球，每串中下面球没击中，上面球不能击中，则把这6个球全部击中射击方法数是（ ）

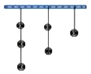
    A.78B.60C.48D.36

    【答案】B

    【解析】

    根据题意，假设6个小球为A、B、C、D、E、F，要求C在B之前，B在A之前，且E在D之间被击中，先不考虑限制条件，计算将6个小球按被击中的顺序排成一排的情况，进而计算ABC、DE之间的顺序，据此分析可得答案．

    解：根据题意，如图：假设6个小球为A、B、C、D、E、F，要求C在B之前，B在A之前，且E在D之前被击中，

    若不考虑限制条件，将6个小球按被击中的顺序排成一排，有A66＝720种情况，

    ABC之间的顺序有A33种，DE之间的顺序有A22种，

    其中C在B之前，B在A之前，且E在D之间，则把这6个球全部击中射击方法数是60种；

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

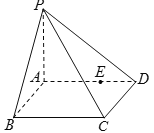
    【题目】如图，四棱锥中，是矩形，平面，，，四棱锥外接球的球心为，点是棱上的一个动点.给出如下命题：①直线与直线所成的角中最小的角为；②与一定不垂直；③三棱锥的体积为定值；④的最小值为.其中正确命题的序号是__________.（将你认为正确的命题序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正项数列：，满足：是公差为的等差数列，是公比为2的等比数列.

    （1）若，求数列的所有项的和；

    （2）若，求的最大值；

    （3）是否存在正整数，满足?若存在，求出的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是菱形，底面，，，点为棱的中点，点分别为棱上的动点(与所在棱的端点不重合），且满足．

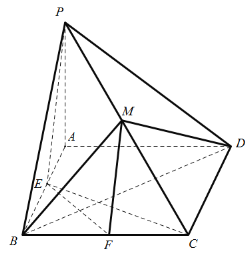
    （1）证明：平面平面;

    （2）当三棱锥的体积最大时，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列{an}中，若an2﹣an﹣12＝p，（n≥2，n∈N*，p为常数），则称{an}为“等方差数列”，下列是对“等方差数列“的判断：

    ①若{an}是等方差数列，则{an2}是等差数列；

    ②{（﹣1）n}是等方差数列；

    ③若{an}是等方差数列，则{akn}（k∈N*，k为常数）也是等方差数列；

    ④若{an}既是等方差数列，又是等差数列，则该数列为常数列．

    其中正确命题的个数是（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】端午节吃粽子是我国的传统习俗，设一盘中装有10个粽子，其中豆沙粽子3个，肉粽子2个，白粽子5个，这三种粽子的外观完全相同，从中任意选取3个．

    （1）求三种粽子各取到1个的概率；

    （2）设ξ表示取到的豆沙粽子个数，求ξ的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知递增数列{an}前n项和为Sn，且满足a1＝3，4Sn﹣4n+1＝an2，设bn（n∈N*)且数列{bn}的前n项和为Tn

    （Ⅰ)求证：数列{an}为等差数列；

    （Ⅱ)若对任意的n∈N*，不等式λTnn（﹣1)n+1恒成立，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某银行推出一款短期理财产品，约定如下：

    （1）购买金额固定；

    （2）购买天数可自由选择，但最短3天，最长不超过10天；

    （3）购买天数与利息的关系，可选择下述三种方案中的一种：

    方案一：；方案二：；方案三：.

    请你根据以上材料，研究下面两个问题：

    （1）结合所学的数学知识和方法，用其它方式刻画上述三种方案的函数特征；

    （2）依据你的分析，给出一个最佳理财方案.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年底，湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者.为及时有效地对疫情数据进行流行病学统计分析，某地研究机构针对该地实际情况，根据该地患者是否有武汉旅行史与是否有确诊病例接触史，将新冠肺炎患者分为四类：有武汉旅行史（无接触史），无武汉旅行史（无接触史），有武汉旅行史（有接触史）和无武汉旅行史（有接触史），统计得到以下相关数据.

    （1）请将列联表填写完整：

    有接触史

    无接触史

    总计

    有武汉旅行史

    27

    无武汉旅行史

    18

    总计

    27

    54

    （2）能否在犯错误的概率不超过0.025的前提下认为有武汉旅行史与有确诊病例接触史有关系？

    附：

    0.15

    0.10

    0.05

    0.025

    0.010

    2.072

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    同步练习册答案