
【题目】若直线ax+by—4=0和圆x2+y2=4没有公共点,则过点(a,b)的直线与椭圆![]() +
+![]() =1的公共点个数为( )
=1的公共点个数为( )
A. 0 B. 1 C. 2 D. 由a,b的取值来确定
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
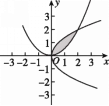
【题目】已知曲线C1:y2=2x与C2:y=![]() x2在第一象限内的交点为P.
x2在第一象限内的交点为P.
(1)求过点P且与曲线C2相切的直线方程;
(2)求两条曲线所围图形(如图所示的阴影部分)的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:

①BD⊥AC; ②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥; ④平面ADC⊥平面ABC。
其中正确的是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,点P,G分别是
中,点P,G分别是![]() ,
,![]() 的中点,已知
的中点,已知![]() ⊥平面ABC,
⊥平面ABC,![]() =
=![]() =3,
=3,![]() =
=![]() =2.
=2.
(I)求异面直线![]() 与AB所成角的余弦值;
与AB所成角的余弦值;
(II)求证:![]() ⊥平面
⊥平面![]() ;
;
(III)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣ ![]() (a>0)
(a>0)
(1)若x=1是函数f(x)的一个极值点,求a的值;
(2)若f(x)≥0在[0,+∞)上恒成立,求a的取值范围;
(3)证明: ![]() (e为自然对数的底数).
(e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求三棱锥E—ABC的体积V.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2-2(a+1)x+2a+a2<0,q:实数x满足![]()
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com