
����Ŀ��ij�綯���ۺ�������С��������г��������ȡ20�����綯������������ʻ��̣����γ�������ʻ�������̣�����������������ʻ���ȫ������50�����300����֮�䣬��ͳ�ƽ���ֳ�5�飺![]() �����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
�����Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.

��1������ʻ�����![]() �ij�������
�ij�������
��2������ʻ��̵�ƽ������
��3��������ʻ�����![]() �ij����������ȡ2������������ǡ��һ��������ʻ�����
�ij����������ȡ2������������ǡ��һ��������ʻ�����![]() �ڵĸ���.
�ڵĸ���.
���𰸡���1��5������2��170����3��![]() .
.
��������
��1���������г��������֮��Ϊ1�����δ֪��![]() �����������
�����������![]() �����ε����֮�ͼ�Ϊ���ʣ��ô����ݳ��������������ɣ�
�����ε����֮�ͼ�Ϊ���ʣ��ô����ݳ��������������ɣ�
��2����ÿ�������ε����������������ױ��е�ֵ������ͼ��ɵõ������
��3���ȼ������![]() �еij������������оٳ����еij�ȡ�����ԣ��ҳ���������Ŀ����ԣ��ùŵ���͵ĸ��ʼ��㹫ʽ�������.
�еij������������оٳ����еij�ȡ�����ԣ��ҳ���������Ŀ����ԣ��ùŵ���͵ĸ��ʼ��㹫ʽ�������.
�������֪��![]()
��![]() ��
��
����ʻ�����![]() �ij�����Ϊ��
�ij�������![]()
��2����ֱ��ͼ�ɵã�
������̵�ƽ����Ϊ��![]() .
.
��3���ɣ�2���������֪����ʻ�����![]() �ij�����Ϊ3���ֱ��Ϊ
�ij�����Ϊ3���ֱ��Ϊ![]() ��
��
��ʻ�����![]() �ij�����Ϊ2���ֱ��Ϊ
�ij�����Ϊ2���ֱ��Ϊ![]() ��
��
�¼�![]() ������ǡ��һ����������ʻ���Ϊ
������ǡ��һ����������ʻ���Ϊ![]() ��
��
�Ӹ�5�������������ȡ2�������еĿ������£�
![]() ��10�������
��10�������
�¼�![]() �����Ŀ����й�
�����Ŀ����й� ![]() 6�������
6�������
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�ƽ��
�У�ƽ��![]() ��ƽ��
��ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() Ϊֱ�����Σ�
Ϊֱ�����Σ�![]() ��
��![]() .
.

��1����֤��ֱ��![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���������⣺�� ��
���������⣺�� ��
������![]() ��ͼ�����ԭ��Գƣ� ������
��ͼ�����ԭ��Գƣ� ������![]() �����ں�����
�����ں�����
����![]() ʱ,����
ʱ,����![]() ȡ���ֵ��������
ȡ���ֵ��������![]() ��ͼ���뺯��
��ͼ���뺯��![]() ��ͼ��û�й����㣬������ȷ����������
��ͼ��û�й����㣬������ȷ����������
��A���٢� ��B���ڢ� ��C���٢� ��D���ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ��˫�����й�ͬ����![]() ��
��![]() �����ǵ�һ�����㣬��
�����ǵ�һ�����㣬��![]() ������Բ��˫���ߵ������ʷֱ�Ϊ
������Բ��˫���ߵ������ʷֱ�Ϊ![]() ����
����![]() �����ֵΪ�� ��
�����ֵΪ�� ��
A. 3B. 2C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ��������M��4����2����N��2��4��.
��1����MN�Ĵ�ֱƽ���߷��̣�
��2��ֱ��l������A��3��0�����ҵ�M�͵�N��ֱ��l�ľ�����ȣ���ֱ��l�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() ������
������![]() ����
Ϊ���Σ�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ���е㣮
���е㣮

![]() 1
1![]() ֤����
֤����![]() ��
��
![]() 2
2![]() ��
��![]() Ϊ
Ϊ![]() �ϵĶ��㣬
�ϵĶ��㣬![]() ��ƽ��
��ƽ��![]() �������ǵ�����ֵΪ
�������ǵ�����ֵΪ![]() ��������
��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ֱ������![]() �У�
�� ![]() ����
����![]() �ֱ���
�ֱ���![]() ���е�.
���е�.
��1����֤�� ![]() ��ƽ��
��ƽ��![]() ��
��
��2����![]() ����֤��
����֤�� ![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC��A1B1C1�У�E��F�ֱ�ΪA1C1��BC���е㣬M��N�ֱ�ΪA1B��A1C���е�.��֤��
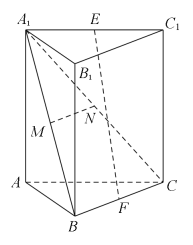
��1��MN��ƽ��ABC��
��2��EF��ƽ��AA1B1B.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��
��![]() �������ڵ�
�������ڵ�![]() ���ұ�
���ұ�![]() �����صõ��ҳ�Ϊ
�����صõ��ҳ�Ϊ![]() ��Բ��
��Բ��![]() �ڵ�һ����.
�ڵ�һ����.
������Բ![]() �ķ��̣�
�ķ��̣�
��������![]() ��ֱ��
��ֱ��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ��Բ
��Բ![]() �����ߣ��е�Ϊ
�����ߣ��е�Ϊ![]() ������
������![]() �������Сʱ��������
�������Сʱ��������![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com