练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    证明：在△ABC中，若∠C是直角，那么∠B一定是锐角.

    证明：假设∠B不是锐角，则∠B是钝角或直角，即∠B≥90°.

    ∵∠C=90°,

    ∴∠B+∠C≥180°.

    又∵∠A＞0°,

    ∴∠A+∠B+∠C＞180°.

    这与∠A+∠B+∠C=180°矛盾.所以假设错误，则∠B一定是锐角.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：哈师大附中2008-2009年度高二下学期第一次月考考试数学试卷　文科 题型：013

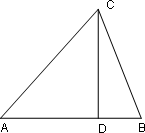
    如图，在△ABC中，AC＞BC，CD是AB边上的高，求证∠ACD＞∠BCD，过程如下：证明：在△ABC中，因为CD⊥AB，AC＞BC，所以AD＞BD，所以∠ACD＞∠BCD，上述证明中错误的是

    [　　]

    A．大前提

    B．小前提

    C．结论

    D．没有错误

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    证明：在△ABC中，（其中R为△ABC的外接圆的半径）.?

     

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　北师大课标高二版(选修2－2)　2009－2010学年　第30期　总第186期 北师大课标 题型：047

    用分析法证明：在△ABC中，若A＋B＝120°，则＋＝1．

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：填空题

    “如图所示，在△ABC中，AC>BC，CD是AB边上的高，求证：∠ACD>∠BCD。”
    证明：在△ABC中，因为CD⊥AB，AC>BC， ①
    所以AD>BD，②
    于是∠ACD>∠BCD。③
    则在上面证明的过程中错误的是（    ）。（只填序号）

    查看答案和解析>>

    同步练习册答案