
【题目】如图,在直四棱柱![]() 中,已知
中,已知![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)设![]() 是
是![]() 上一点,试确定
上一点,试确定![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由.
,并说明理由.
【答案】⑴连DC1,正方形DD1C1C中,D1C⊥C1D
∵AD⊥平面DD1C1C ∴AD⊥CD1又AD∩CD1=D
∴CD1⊥平面DA C1![]()
⑵ E 为AC中点时,![]() 平面
平面![]() 9’
9’
梯形ABCD中,DE∥且=" AB " ∴AD∥且=BE
∵AD∥且= A1D1∴A1D1∥且="BE " ∴A1D1EB是平行四边形
∴D1E∥B A1又B A1![]() 平面DB A1D1E
平面DB A1D1E![]() 平面DB A1
平面DB A1
∴![]() 平面
平面![]()
【解析】试题分析:
(1)本题为证线与线垂直,常规思路为转化为证线与另一条
直线所在的平面垂直。结合条件,可证出![]() 平面
平面![]() ,则得:
,则得:![]() .
.
(2)本题为通过确定点![]() 的位置来证明证线与面平行,可通过题中的条件进行大胆设想,(
的位置来证明证线与面平行,可通过题中的条件进行大胆设想,(![]() 为中点),然后进行对应的证明,可解决;
为中点),然后进行对应的证明,可解决;
试题解析:
(1)在直四棱柱![]() 中,
中,
连结![]() ,
,![]() ,
,![]() 四边形
四边形![]() 是正方形.
是正方形.![]() .
.
又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() .
.![]() 平面
平面![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() .
.
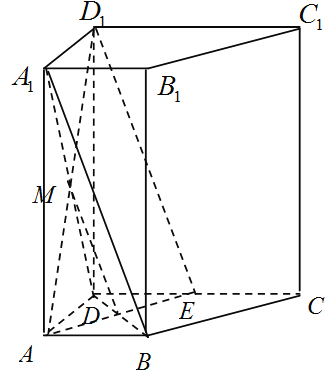
(2)连结![]() ,连结
,连结![]() ,设
,设![]() ,
,
![]() ,连结
,连结![]() ,
,![]() 平面
平面![]() 平面
平面![]() ,
,
要使![]() 平面
平面![]() ,须使
,须使![]() ,
,
又![]() 是
是![]() 的中点.
的中点.![]() 是
是![]() 的中点.
的中点.
又易知![]() ,
,![]() .
.
即![]() 是
是![]() 的中点.综上所述,当
的中点.综上所述,当![]() 是
是![]() 的中点时,可使
的中点时,可使![]() 平面
平面![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】在一个6×6的表格中放3颗完全相同的白棋和3颗完全相同的黑棋,若这6颗棋子不在同一行也不在同一列上,则不同的放法有( )
A.14400种
B.518400种
C.720种
D.20种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出一个用循环语句编写的程序:
k=1
sum=0
WHILE k<10
sum=sum+k∧2
k=k+1
WEND
PRINT sum
END
(1)指出程序所用的是何种循环语句,并指出该程序的算法功能;
(2)请用另一种循环语句的形式把该程序写出来.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关,通过随机抽查110名学生,得到如下2×2的列联表:
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式K2= ![]() ,算得K2≈7.61
,算得K2≈7.61
附表:
p(K2≥k0) | 0.025 | 0.01 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
参照附表,以下结论正确是( )
A.有99.5%以上的把握认为“爱好该项运动与性别有关”
B.有99.5%以上的把握认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是异面直线,则以下四个命题:①存在分别经过直线
是异面直线,则以下四个命题:①存在分别经过直线![]() 和
和![]() 的两个互相垂直的平面;②存在分别经过直线
的两个互相垂直的平面;②存在分别经过直线![]() 和
和![]() 的两个平行平面;③经过直线
的两个平行平面;③经过直线![]() 有且只有一个平面垂直于直线
有且只有一个平面垂直于直线![]() ;④经过直线
;④经过直线![]() 有且只有一个平面平行于直线
有且只有一个平面平行于直线![]() ,其中正确的个数有( )
,其中正确的个数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|< ![]() )的图象过点B(0,﹣1),且在(
)的图象过点B(0,﹣1),且在( ![]() ,
, ![]() )上单调,同时f(x)的图象向左平移π个单位之后与原来的图象重合,当x1 , x2∈(﹣
)上单调,同时f(x)的图象向左平移π个单位之后与原来的图象重合,当x1 , x2∈(﹣ ![]() ,﹣
,﹣ ![]() ),且x1≠x2时,f(x1)=f(x2),则f(x1+x2)=( )
),且x1≠x2时,f(x1)=f(x2),则f(x1+x2)=( )
A.﹣ ![]()
B.﹣1
C.1
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】<中华人民共和国个人所得税法>规定,公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额,此项税款按下表分段累计计算:

(1)若某人一月份应缴纳此项税款为280元,那么他当月的工资、薪金所得是多少?
(2)假设某人一个月的工资、薪金所得是![]() 元(0<
元(0<![]() 10000),试将其当月应缴纳此项税款
10000),试将其当月应缴纳此项税款![]() 元表示成关于
元表示成关于![]() 的函数.
的函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从6名学生会干部(其中男生4人,女生2人)中选3人参加青年联合会志愿者。
(1)设所选3人中女生人数为 ![]() ,求
,求 ![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com