
【题目】直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,D是AB的中点.
(Ⅰ)求证:AC⊥B1C;
(Ⅱ)求证:AC1∥平面B1CD
【答案】证明:(Ⅰ)在△ABC中,因为AB=5,AC=4,BC=3,
所以AC⊥BC.
因为直三棱柱ABC﹣A1B1C1 , 所以,CC1⊥AC.
因为BC∩AC=C,所以AC⊥平面BB1C1C.
所以AC⊥B1C.
(Ⅱ)连接BC1 , 交B1C于E.
因为直三棱柱ABC﹣A1B1C1 ,
所以侧面BB1C1C为矩形,且E为B1C中点.
又D是AB中点,所以DE为△ABC1的中位线,所以DE∥AC1 .
因为DE平面B1CD,AC1平面B1CD,
所以,AC1∥平面B1CD.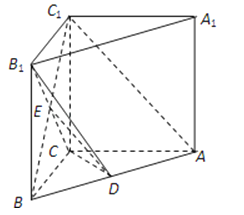
【解析】(Ⅰ) 利用勾股定理可得AC⊥BC,由直三棱柱的性质可得CC1⊥AC,从而得到AC⊥平面BB1C1C,进而得到AC⊥B1C.
(Ⅱ) 取B1C中点E,得到 DE为△ABC1的中位线,得到DE∥AC1 , 由线面平行的判定定理证得AC1∥平面B1CD.


科目:高中数学 来源: 题型:
【题目】8人排成一排照相,分别求下列条件下的不同照相方式的种数.
(1)其中甲、乙相邻,丙、丁相邻;
(2)其中甲、乙不相邻,丙、丁不相邻;
(要求写出解答过程,并用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cos A=![]() ,B=A+
,B=A+![]() .
.
(1)求b的值;
(2)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间四边形PABC的各边及对角线长度都相等,D、E、F、G分别是AB、BC、CA、AP的中点,下列四个结论中成立的是
①BC∥平面PDF
②DF⊥平面PAE
③平面GDF∥平面PBC
④平面PAE⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
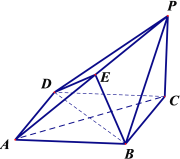
【题目】如图,在四棱锥![]() 中, 底面
中, 底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 平面
平面![]() ,求证:
,求证:![]() ;
;
(Ⅲ)是否存在点![]() ,使得四面体
,使得四面体![]() 的体积等于四面体
的体积等于四面体![]() 的体积的
的体积的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两定点![]() ,
, ![]() 和一动点
和一动点![]() ,给出下列结论:
,给出下列结论:
①若![]() ,则点
,则点![]() 的轨迹是椭圆;
的轨迹是椭圆;
②若![]() ,则点
,则点![]() 的轨迹是双曲线;
的轨迹是双曲线;
③若![]() ,则点
,则点![]() 的轨迹是圆;
的轨迹是圆;
④若![]() ,则点
,则点![]() 的轨迹关于原点对称;
的轨迹关于原点对称;
⑤若直线![]() 与
与![]() 斜率之积等于
斜率之积等于![]() ,则点
,则点![]() 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).
其中正确的是__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假,并说明理由.
(1)x∈R,都有x2-x+1>![]() ;
;
(2)α,β,使cos(α-β)=cos α-cos β;
(3)x,y∈N,都有(x-y)∈N;
(4)x,y∈Z,使![]() x+y=3.
x+y=3.
查看答案和解析>>
科目:高中数学 来源: 题型:
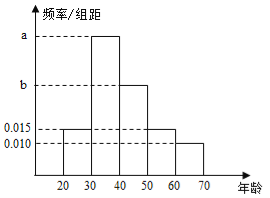
【题目】【广西南宁2017届高三检测】根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
(1)已知![]() 、
、![]() ,
,![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() ,
,![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券,已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com