
【题目】已知f(x)=max{x2﹣ax+a,ax﹣a+1},其中max{x,y}= ![]() . (Ⅰ)若对任意x∈R,恒有f(x)=x2﹣ax+a,求实数a的值;
. (Ⅰ)若对任意x∈R,恒有f(x)=x2﹣ax+a,求实数a的值;
(Ⅱ)若a>1,求f(x)的最小值m(a).
【答案】解:(Ⅰ)由对任意x∈R,恒有f(x)=x2﹣ax+a, ∴对 x∈R时,x2﹣ax+a≥ax﹣a+1恒成立,
即x2﹣2ax+2a﹣1≥0恒成立
∴△=4a2﹣4(2a﹣1)≤0,即(a﹣1)2≤0,
∴a=1,
实数a的值1;
(Ⅱ)若x2﹣2ax+a≥ax﹣a+1,则x2﹣2ax+2a﹣1≥0,即(x﹣1)[x﹣(2a﹣1)]≥0,
∵a>1,
∴2a﹣1>1,
∴不等式的解为:x≤1或x≥2a﹣1,
∴f(x)= 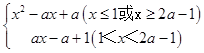 ,
,
①当 ![]() ≤1,即1<a≤2 时,f(x)在(﹣∞,
≤1,即1<a≤2 时,f(x)在(﹣∞, ![]() ) 递减,在(
) 递减,在( ![]() ,+∞)递增,
,+∞)递增,
∴f(x)的最小值m(a)=f( ![]() )=﹣
)=﹣ ![]() +a,
+a,
②当 ![]() >1,即a>2 时,f(x)在(﹣∞,1)递减,在(1,+∞)递增
>1,即a>2 时,f(x)在(﹣∞,1)递减,在(1,+∞)递增
∴f(x)的最小值m(a)=f(1)=1,
∴m(a)= 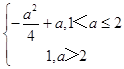
【解析】(Ⅰ)由题意可知:对 x∈R时,x2﹣ax+a≥ax﹣a+1恒成立,整理可知:x2﹣2ax+2a﹣1≥0恒成立根据二次函数性质可知:△<0,即可求得a的值;(Ⅱ)由当x2﹣2ax+a≥ax﹣a+1,即(x﹣1)[x﹣(2a﹣1)]≥0,由a>1,则2a﹣1>1,因此不等式的解为:x≤1或x≥2a﹣1,分类当 ![]() ≤1,即1<a≤2 时及当
≤1,即1<a≤2 时及当 ![]() >1,即a>2 时,根据函数的单调性即可求得f(x)的最小值m(a)的表达式.
>1,即a>2 时,根据函数的单调性即可求得f(x)的最小值m(a)的表达式.
【考点精析】关于本题考查的函数的最值及其几何意义和二次函数的性质,需要了解利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能得出正确答案.
上递减才能得出正确答案.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,已知x≥0时,f(x)=x2﹣2x. 
(1)画出偶函数f(x)的图像的草图,并求函数f(x)的单调递增区间;
(2)当直线y=k(k∈R)与函数y=f(x)恰有4个交点时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按![]() 元/度收费,超过200度但不超过400度的部分按
元/度收费,超过200度但不超过400度的部分按![]() 元/度收费,超过400度的部分按1.0元/度收费.
元/度收费,超过400度的部分按1.0元/度收费.

(Ⅰ)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(Ⅱ)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅲ)在满足(Ⅱ)的条件下,若以这100户居民用电量的频率代替该月全市居民用户用电量的概率,且同组中的数据用该组区间的中点代替,记![]() 为该居民用户1月份的用电费用,求
为该居民用户1月份的用电费用,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三名学生参加某电视台举办的国学知识竞赛,在本次竞赛中只有过关和不过关两种结果,假设甲、乙、丙竞赛过关的概率分别为![]() ,且他们竞赛过关与否互不影响.
,且他们竞赛过关与否互不影响.
(1)求在这次国学知识竞赛中,甲、乙、丙三名学生至少有一名学生过关的概率;
(2)记在这次国学知识竞赛中,甲、乙、丙三名学生过关的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了了解全校学生的阅读情况,在全校采用随机抽样的方法抽取了60名学生(其中初中组和高中组各30名)进行问卷调查,并将他们在一个月内去图书馆的次数进行了统计,将每组学生去图书馆的次数分为5组: ![]() ,分别制作了如图所示的频率分布表和频率分布直方图.
,分别制作了如图所示的频率分布表和频率分布直方图.
分组 | 人数 | 频率 |
| 3 | |
| 9 | |
| 9 | |
| 0.2 | |
| 0.1 |
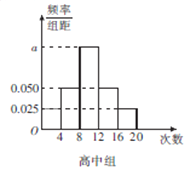
(1)完成频率分布表,并求出频率分布直方图中![]() 的值;
的值;
(2)在抽取的60名学生中,从在一个月内去图书馆的次数不少于16次的学生中随机抽取3人,并用![]() 表示抽得的高中组的人数,求
表示抽得的高中组的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.
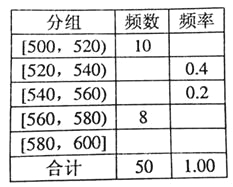
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )
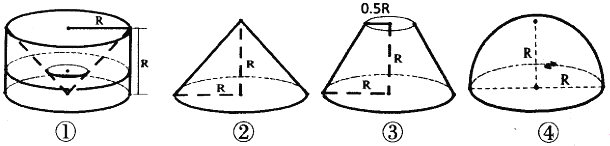
A. ①② B. ①③ C. ②④ D. ①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com