
某单位最近组织了一次健身活动,参加活动的职工分为登山组和游泳组,且每个职工至多参加其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的 ,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组中不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定
,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组中不同年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定
(1)游泳组中青年人、中年人、老年人分别所占的比例.
(2)游泳组中青年人、中年人、老年人分别应抽取的人数.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下所示:
| | 又发作过心脏病 | 未发作过心脏病 | 合计 |
| 心脏搭桥手术 | 39 | 157 | 196 |
| 血管清障手术 | 29 | 167 | 196 |
| 合计 | 68 | 324 | 392 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下面给出某村委调查本村各户收入情况所作的抽样,阅读并回答问题:
①本村人口:1200人;户数300户,每户平均人口数4人
②应抽户数:30
③抽样间隔: =40
=40
④确定随机数字:取一张人民币,后两位数为12
⑤确定第一样本户:编号为12的户为第一样本户
⑥确定第二样本户:12+40=52,52号为第二样本户
⑦……
(1) 该村委采用了何种抽样方法?
(2) 抽样过程存在哪些问题,试改之;
(3) 何处用的是简单随机抽样?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为缓解某路段交通压力,计划将该路段实施“交通限行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
| 年龄 (岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频 数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成 人数 | 4 | 8 | 9 | 6 | 4 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为调查甲、乙两校高三年级学生某次联考数学成绩情况,用简单随机抽样,从这两校中各抽取30名高三年级学生,以他们的数学成绩(百分制)作为样本,样本数据的茎叶图如图.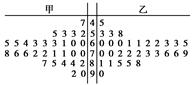
(1)若甲校高三年级每位学生被抽取的概率为0.05,求甲校高三年级学生总人数,并估计甲校高三年级这次联考数学成绩的及格率(60分及60分以上为及格);
(2)设甲、乙两校高三年级学生这次联考数学平均成绩分别为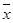 1,
1,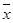 2,估计
2,估计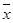 1-
1-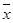 2的值.
2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
研究性学习小组为了解某生活小区居民用水量 (吨)与气温
(吨)与气温 (℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
(℃)之间的关系,随机统计并制作了5天该小区居民用水量与当天气温的对应表:
| 日期 | 9月5日 | 10月3日 | 10月8日 | 11月16日 | 12月21日 |
气温 (℃) (℃) | 18 | 15 | 11 | 9 | -3 |
用水量 (吨) (吨) | 57 | 46 | 36 | 37 | 24 |
 中的
中的 ,试求出
,试求出 的值,并预测当地气温为5℃时,该生活小区的用水量.
的值,并预测当地气温为5℃时,该生活小区的用水量.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两所学校高三年级分别有1 200人,1 000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| | | | | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
| | 甲校 | 乙校 | 总计 |
| 优秀 | | | |
| 非优秀 | | | |
| 总计 | | | |
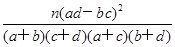 . ?
. ?| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(1)求n的值;
(2)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖,.求a和b至少有一人上台抽奖的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以 表示.
表示.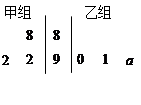
(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求 的值;
的值;
(Ⅱ)求乙组平均成绩超过甲组平均成绩的概率;
(Ⅲ)当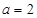 时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com