
【题目】(本小题满分10分)已知![]() 是公差不为零的等差数列,
是公差不为零的等差数列, ![]() ,且
,且![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项;
的通项;
(2)求数列![]() 的前n项和.
的前n项和.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设数列![]() 的公差为
的公差为![]() ,由
,由![]() ,且
,且![]() 成等比数列,可得
成等比数列,可得![]() ,即
,即![]() ,解出
,解出![]() 即可得出通项公式;(2)由(1)可得
即可得出通项公式;(2)由(1)可得![]() ,
, ![]() ,根据等比数列的前
,根据等比数列的前![]() 项和公式利用错位相减法求和即可.
项和公式利用错位相减法求和即可.
试题解析:(1)数列![]() 的公差为
的公差为![]() ,由
,由![]() ,且
,且![]() 成等比数列,可得
成等比数列,可得![]() ,即
,即![]() ,可得
,可得![]()
(2)![]()
![]()
-得:![]()
∴![]()
【易错点晴】本题主要考查等差数列的通项公式、等比数列的求和公式以及“错位相减法”求数列的和,属于中档题. “错位相减法”求数列的和是重点也是难点,利用“错位相减法”求数列的和应注意以下几点:①掌握运用“错位相减法”求数列的和的条件(一个等差数列与一个等比数列的积);②相减时注意最后一项 的符号;③求和时注意项数别出错;④最后结果一定不能忘记等式两边同时除以![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
(1)求A,(RA)∩B;
(2)若A∪C=R,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在区间
在区间![]() 上,
上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均可为一个三角形的三边长,则称函数
均可为一个三角形的三边长,则称函数![]() 为“三角形函数”.已知函数
为“三角形函数”.已知函数![]() 在区间
在区间![]() 上是“三角形函数”,则实数
上是“三角形函数”,则实数![]() 的取值范围为( )
的取值范围为( )
A. 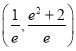 B.
B. ![]()
C. ![]() D.
D. 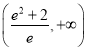
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大理石工厂初期花费98万元购买磨大理石刀具,第一年需要各种费用12万元,从第二年起,每年所需费用比上一年增加4万元,该大理石加工厂每年总收入50万元.
(1)到第几年末总利润最大,最大值是多少?
(2)到第几年末年平均利润最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 共焦点
共焦点![]() ,抛物线上的点M到y轴的距离等于
,抛物线上的点M到y轴的距离等于![]() ,且椭圆与抛物线的交点Q满足
,且椭圆与抛物线的交点Q满足![]() .
.
(I)求抛物线的方程和椭圆的方程;
(II)过抛物线上的点![]() 作抛物线的切线
作抛物线的切线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,求此切线在x轴上的截距的取值范围.
两点,求此切线在x轴上的截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某举重运动队为了解队员的体重分布情况,从50名队员中抽取10名作调查.抽取时现将全体队员随机按1~50编号,并按编号顺序平均分成10组,每组抽一名,且各组内抽取的编号依次增加5进行系统抽样.
(1)若第5组抽出的号码为22,写出所有被抽取出来的编号;
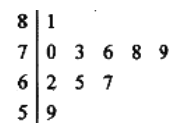
(2)分别统计被抽取的10名队员的体重(单位:公斤),获得如图所示的体重数据的茎叶图,根据茎叶图求该样本的平均数和中位数;
(3)在题(2)的茎叶图中,从题中不轻于73公斤的队员中随机抽取2名队员的体重数据,求体重为81公斤的队员被抽到的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线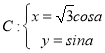 (
(![]() 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线的极坐标方程为:
轴的非负半轴为极轴建立的极坐标系中,直线的极坐标方程为: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线的直角坐标方程;
的普通方程和直线的直角坐标方程;
(Ⅱ)过点![]() 且与直线平行的直线
且与直线平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求点
两点,求点![]() 到
到![]() ,
, ![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com