
【题目】设![]() 函数
函数![]() 为
为![]() 的导函数
的导函数
(1)若曲线![]() 与曲线
与曲线![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)设函数![]() 若
若![]() 为函数
为函数![]() 的极大值,且
的极大值,且![]()
①求![]() 的值;
的值;
②求证:对于![]() .
.
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() ,对于任意实数k,下列直线被椭圆E截得的弦长与l:y=kx+1被椭圆E截得的弦长不可能相等的是( )
,对于任意实数k,下列直线被椭圆E截得的弦长与l:y=kx+1被椭圆E截得的弦长不可能相等的是( )
A. kx+y+k=0 B. kx-y-1=0
C. kx+y-k=0 D. kx+y-2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为侧棱
为侧棱![]() 上一点.
上一点.

(1)若![]() ,求证:
,求证:![]()
![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在侧棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ? 若存在,求出线段
? 若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C:y=
中,曲线C:y=![]() 与直线
与直线![]() (
(![]() >0)交与M,N两点,
>0)交与M,N两点,
(Ⅰ)当k=0时,分别求C在点M和N处的切线方程;
(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是 _________ .

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应国家提出的“大众创业,万众创新”的号召,小李同学大学毕业后,决定利用所学专业进行自主创业。经过市场调查,生产某小型电子产品需投入年固定成本为5万元,每年生产![]() 万件,需另投入流动成本为
万件,需另投入流动成本为![]() 万元,且
万元,且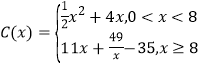 ,每件产品售价为10元。经市场分析,生产的产品当年能全部售完。
,每件产品售价为10元。经市场分析,生产的产品当年能全部售完。
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万件)的函数解析式;
(万件)的函数解析式;
(注:年利润=年销售收入-固定成本-流动成本)
(2)年产量为多少万件时,小李在这一产品的生产中所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过右焦点作垂直于椭圆长轴的直线交椭圆于
,过右焦点作垂直于椭圆长轴的直线交椭圆于![]() 两点,且
两点,且![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2) 设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() .
.
①求![]() 的值;
的值;
②求![]() 的面积
的面积![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3名男生,4名女生,按照不同的要求排队,求不同的排队方案的方法种数.(要求每问要有适当的分析过程,列式并算出答案)
(1)选其中5人排成一排;
(2)排成前后两排,前排3人,后排4人;
(3)全体站成一排,男、女各站在一起;
(4)全体站成一排,男生不能站在一起;
(5)全体站成一排,甲不站排头也不站排尾.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com