
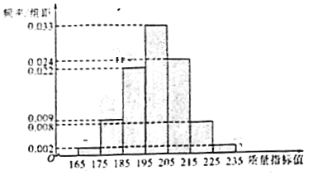
����Ŀ����ij��ҵ������ij�ֲ�Ʒ�г�ȡ![]() ����������Щ��Ʒ��һ������ָ��ֵ���ɲ����������Ƶ�ʷֲ�ֱ��ͼ��
����������Щ��Ʒ��һ������ָ��ֵ���ɲ����������Ƶ�ʷֲ�ֱ��ͼ��
��1������![]() ����Ʒ����ָ��ֵ������ƽ����
����Ʒ����ָ��ֵ������ƽ����![]() ����������
����������![]() ��ͬһ���е������ø���������е�ֵ����������
��ͬһ���е������ø���������е�ֵ����������
��2����ֱ��ͼ������Ϊ�����ֲ�Ʒ������ָ��ֵ![]() ������̬�ֲ�
������̬�ֲ�![]() ������
������![]() ����Ϊ����ƽ����
����Ϊ����ƽ����![]() ��
��![]() ������������
������������![]() .
.
�����ø���̬�ֲ�����![]() ��
��
��ij�û��Ӹ���ҵ������![]() �����ֲ�Ʒ����
�����ֲ�Ʒ����![]() ��ʾ��
��ʾ��![]() ����Ʒ������ָ��ֵλ������
����Ʒ������ָ��ֵλ������![]() �IJ�Ʒ����.���âٵĽ������
�IJ�Ʒ����.���âٵĽ������![]() .
.
����![]() .��
.��![]() ����
����![]() ��
��![]() .
.
���𰸡���1��![]() ��
��![]() ����2��68.26
����2��68.26
�����������������������������ɢ����������������ͷ��ʽ�������������������i���ɣ�����֪Z��N��200��150�����Ӷ����P��187��8��Z��212��2����ע�������������ݣ���ii���ɣ�i��֪X��B��100��0��6826��������EX=np�������
�����������1����ȡ��Ʒ������ָ��ֵ������ƽ����![]() ����������s2�ֱ�Ϊ
����������s2�ֱ�Ϊ
![]() ��170��0��02��180��0��09��190��0��22��200��0��33��210��0��24��220��0��08��230��0��02��200��
��170��0��02��180��0��09��190��0��22��200��0��33��210��0��24��220��0��08��230��0��02��200��
s2������30��2��0��02������20��2��0��09������10��2��0��22��0��0��33��102��0��24��202��0��08��302��0��02��150����6��
��2����i���ɣ�1��֪��Z��N��200��150����
�Ӷ�P��187��8��Z��212��2����P��200��12��2��Z��200��12��2����0��682 6��
��ii���ɣ�i��֪��һ����Ʒ������ָ��ֵλ�����䣨187��8��212��2���ĸ���Ϊ0��682 6��
������֪X��B��100��0��682 6����
����EX��100��0��682 6��68��26��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ں���f��x��������������������Ա�����ֵx1 �� x2 �� ��x1��x2ʱ������f��x1����f��x2�����Ҵ�����������ȵ��Ա���ֵy1 �� y2 �� ʹ��f��y1��=f��y2�����ͳ�f��x��Ϊ�������ϵIJ��ϸ����������
�� �� �� ��
�� �� ��
��
�� �� ��
�� ��![]() ��
��
�ĸ�������Ϊ���ϸ����������� ������֪����g��x���Ķ�����ֵ��ֱ�ΪA��B��A={1��2��3}��BA����g��x��Ϊ������A�ϵIJ��ϸ������������ô������g��x���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P1��a1 �� b1����P2��a2 �� b2��������Pn��an �� bn����n��N*�����ں���y=![]() ��ͼ���ϣ�
��ͼ���ϣ�
����������{bn}�ǵȲ����У���֤����{an}Ϊ�ȱ����У�
����������{an}��ǰn���ΪSn=1��2��n �� ����Pn �� Pn+1��ֱ��������������Χ�����������Ϊcn �� ��ʹcn��t��n��N*�������ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��������
��������![]() �ڵ�
�ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() ��
��
��1����ʵ��![]() ��ֵ������
��ֵ������![]() �����ֵ��
�����ֵ��
��2��֤�����������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㣺 ![]() �����磺34=3������2��4=4������f��x��=x2��2x��x2�������ֵΪ ��
�����磺34=3������2��4=4������f��x��=x2��2x��x2�������ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㣺 ![]() �����磺34=3������2��4=4������f��x��=x2��2x��x2�������ֵΪ ��
�����磺34=3������2��4=4������f��x��=x2��2x��x2�������ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ����һ�ۿڣ����Һ���
����һ�ۿڣ����Һ���![]() ͬʱ�Ӹۿ�
ͬʱ�Ӹۿ�![]() �������������������ٺ��У�����
�������������������ٺ��У�����![]() �ĺ����ٶ�Ϊ20����/Сʱ������
�ĺ����ٶ�Ϊ20����/Сʱ������![]() �ĺ����ٶȴ��ں���
�ĺ����ٶȴ��ں���![]() ���ڸۿ�
���ڸۿ�![]() ��ƫ��60�������ϵ�
��ƫ��60�������ϵ�![]() ����һ�۲�վ��1Сʱ����
����һ�۲�վ��1Сʱ����![]() ������뺣��
������뺣��![]() �ľ���Ϊ30�����
�ľ���Ϊ30�����![]() �������Һ���
�������Һ���![]() ��
��![]() ���ӽ�Ϊ30����
���ӽ�Ϊ30����

��1����۲�վ![]() ���ۿ�
���ۿ�![]() �ľ��룻
�ľ��룻
��2������![]() �ĺ����ٶȣ�
�ĺ����ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʹ��֧��������֧���Ѿ���Ϊ�������������Ҫ������֧����ʽ��ij����ͨ��ͳ�Ʒ���һ���ڳ���ÿ��ľ�����![]() (��Ԫ)��ÿ��ʹ��֧��������֧��������
(��Ԫ)��ÿ��ʹ��֧��������֧��������![]() (ǧ��)����������ع�ϵ�����õ����һ��
(ǧ��)����������ع�ϵ�����õ����һ��![]() ��7���������±�����������Ϊ��������.
��7���������±�����������Ϊ��������.

(1)����ɢ��ͼ��������ع鷽��![]() (
(![]() ��
��![]() ��ȷ��
��ȷ��![]() )��
)��

(2)����Ϊ�˴̼���һ���ѣ�������һ��չʹ��֧��������֧������齱����ܽ���7��Ԫ.�����г����飬�齱���ʹʹ��֧��������֧��������������7ǧ�ˣ��Ծ��߳����Ƿ��б�Ҫ��
չ�齱���
(3)���й��������:����һ�����գ����ڶ���ľ������ǰһ�������������ɣ����ȫ��Ա�����н�������(��)�ľ����£���ȫ��Ա�����������ý����ĸ���.
�����: ![]() ��
��![]() ��
��![]() ��
��![]() .
.
�ο���ʽ��![]() ��
�� ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪����![]() :ʵ��
:ʵ��![]() ����
����![]() ������
������![]() :ʵ��
:ʵ��![]() ���㷽��
���㷽��![]() ��ʾ�Ľ�����
��ʾ�Ľ�����![]() ���ϵ���Բ����
���ϵ���Բ����![]() ��
��![]() �ij�ֲ���Ҫ��������ʵ��
�ij�ֲ���Ҫ��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������![]() :����
:����![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ⼯��
�Ľ⼯��![]() ��
��![]() :����
:����![]() �Ķ�����Ϊ
�Ķ�����Ϊ![]() .��
.��![]() �������⣬
�������⣬![]() �Ǽ����⣬��ʵ��
�Ǽ����⣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com