
分析 (1)将点(4,-4)代入抛物线y2=2px(p>0)可得p值,利用抛物线的定义,求d+|MD|的最小值;
(2)根据线段AB的中点为N(2,$\frac{1}{3}$),利用点差法,求出直线斜率,可得直线l的方程.
解答 解:(1)抛物线C:y2=2px(p>0)经过点(4,-4),可得p=2,
抛物线的准线方程为x=-1,
d+|MD|=|MF|+|MD|≥|DF|=$\sqrt{(1+1)^{2}+(0-3)^{2}}$=$\sqrt{13}$,
∴d+|MD|的最小值为$\sqrt{13}$;
(2)设A(x1,y1),B(x2,y2),
代入抛物线方程,两式相减得:(y1+y2)(y1-y2)=4(x1-x2),
∴直线l的斜率k=$\frac{4}{2×\frac{1}{3}}$=6,
故直线l的方程为y-$\frac{1}{3}$=6(x-2),
即18x-3y-35=0.
点评 本题考查的知识点是直线与抛物线的位置关系,抛物线的标准方程,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
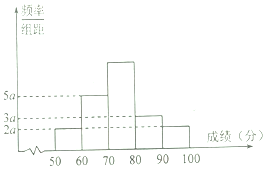 某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.
某学习小组20名学生一次数学考试成绩(单位:分)频率直方图如图所示,已知前三个矩形框垂直于横轴的高度成等差数列.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com