【题目】设函数f（x）= 
，函数y=f[f（x）]﹣1的零点个数为 ．
【答案】2
【解析】解：∵函数 f（x）= 
， 当x≤0时
y=f[f（x）]﹣1=f（2x）﹣1= 
﹣1=x﹣1
令y=f[f（x）]﹣1=0，x=1（舍去）
当0＜x≤1时
y=f[f（x）]﹣1=f（log2x）﹣1= 
﹣1=x﹣1
令y=f[f（x）]﹣1=0，x=1
当x＞1时
y=f[f（x）]﹣1=f（log2x）﹣1=log2（log2x）﹣1
令y=f[f（x）]﹣1=0，log2（log2x）=1
则log2x=2，x=4
故函数y=f[f（x）]﹣1的零点个数为2个
所以答案是：2
【考点精析】利用函数的零点对题目进行判断即可得到答案，需要熟知函数的零点就是方程的实数根，亦即函数的图象与轴交点的横坐标．即：方程有实数根，函数的图象与坐标轴有交点，函数有零点．
科目：高中数学 来源： 题型：
【题目】如图，四边形ABCD与BDEF均为菱形，∠DAB=∠DBF=60°，且FA=FC． （Ⅰ）求证：AC⊥平面BDEF；
（Ⅱ）求证：FC∥平面EAD；
（Ⅲ）求二面角A﹣FC﹣B的余弦值．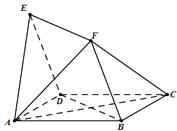
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列 {an} 的前 n 项和为Sn ， S1=6，S2=4，Sn＞0且S2n ， S2n﹣1 ， S2n+2成等比数列，S2n﹣1 ， S2n+2 ， S2n+1成等差数列，则a2016等于（ ）
A.﹣1009
B.﹣1008
C.﹣1007
D.﹣1006
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线C 的参数方程为 
（α为参数），以直角坐标系原点O 为极点，x 轴正半轴为极轴建立极坐标系． （Ⅰ）求曲线C 的极坐标方程；
（Ⅱ）设l1：θ= 
，l2：θ= 
，若l 1、l2与曲线C 相交于异于原点的两点 A、B，求△AOB的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】△ABC中，角A，B，C所对边分别是a、b、c，且cosA= 
．
（1）求sin2 
+cos2A的值；
（2）若a= 
，求△ABC面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若函数 
，为了得到函数g（x）=sin2x的图象，则只需将f（x）的图象（ ）
A.向右平移 
个长度单位
B.向右平移 
个长度单位
C.向左平移 个长度单位
D.向左平移 个长度单位
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某工厂生产某种产品的产量x（吨）与相应的生产成本y（万元）有如下几组样本数据：
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3.1 | 3.9 | 4.5 |
据相关性检验，这组样本数据具有线性相关关系，通过线性回归分析，求得到其回归直线的斜率为0.8，则当该产品的生产成本是6.7万元时，其相应的产量约是（ ）
A.8
B.8.5
C.9
D.9.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
