练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若存在正实数x，y使得x2+y2（lny-lnx）-axy=0（a∈R）成立，则a的取值范围是（　　）

    A. B. C. D.

    【答案】B

    【解析】

    存在性问题转化为有解问题求解，利用到函数研究其单调性求解最小可得a的范围；

    解：由x2+y2（lny-lnx）-axy=0（a∈R）成立，可得x＞0，y＞0；

    同时除以xy，

    可得 存在实数解；

    令，

    可得函数，

    令，

    可得t=1，

    当t在（0，1）时，f′（t）＜0，那么f（t）在（0，1）上单调递减；

    当t在（1，+∞）时，f′（t）＞0，那么f（t）在（1，+∞）上单调递增；

    ∴f（t）min=f（1）=1；

    使得x2+y2（lny-lnx）-axy=0（a∈R）存在实数解，

    则a≥1，

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，椭圆：上的动点到一个焦点的最远距离与最近距离分别是与，的左顶点为与轴平行的直线与椭圆交于、两点，过、两点且分别与直线、垂直的直线相交于点.

    （1）求椭圆的标准方程；

    （2）证明点在一条定直线上运动，并求出该直线的方程；

    （3）求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】记焦点在同一条轴上且离心率相同的椭圆为“相似椭圆”．已知椭圆，以椭圆的顶点焦点为作相似椭圆．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设直线与椭圆交于，两点，且与椭圆仅有一个公共点，试判断的面积是否为定值（为坐标原点）？若是，求出该定值；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，，M是线段EF的中点，二面角的大小为60°.

    （1）求证：平面BDE；

    （2）试在线段AC上找一点P，使得PF与CD所成的角是60°.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地统计局就该地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图(每个分组包括左端点，不包括右端点，如第一组表示收入在[1000,1500))．

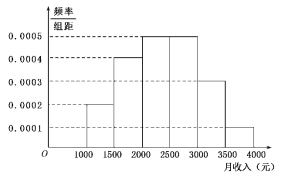
    (1)求居民月收入在[2000,2500)的频率；

    (2)根据频率分布直方图算出样本数据的中位数；

    (3)在月收入为[2500,3000),[3000,3500),[3500,4000]的三组居民中，采用分层抽样方法抽出90人作进一步分析，则月收入在[3000,3500)的这段应抽多少人？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在长方体中，，点为线段上的动点，则下列结论正确的是（ ）

    A.当时，三点共线

    B.当时，

    C.当时，平面

    D.当时，平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知三棱柱中，平面，于点，点在棱上，满足.

    若，求证:平面;

    设平面与平面所成的锐二面角的大小为，若，试判断命题“”的真假，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列中，，是数列的前项和，且．

    （1）求，，并求数列的通项公式；

    （2）设，数列的前项和为，若对任意的正整数都成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某乐园按时段收费，收费标准为：每玩一次不超过小时收费10元，超过小时的部分每小时收费元（不足小时的部分按小时计算）．现有甲、乙二人参与但都不超过小时，甲、乙二人在每个时段离场是等可能的。为吸引顾客，每个顾客可以参加一次抽奖活动。

    (1) 用表示甲乙玩都不超过小时的付费情况，求甲、乙二人付费之和为44元的概率；

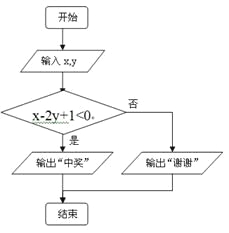
    (2)抽奖活动的规则是：顾客通过操作按键使电脑自动产生两个[0，1]之间的均匀随机数，并按如右所示的程序框图执行．若电脑显示“中奖”，则该顾客中奖；若电脑显示“谢谢”，则不中奖，求顾客中奖的概率．

    查看答案和解析>>

    同步练习册答案