
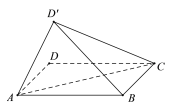
【题目】如图,在矩形![]() 中,将
中,将![]() 沿
沿![]() 翻折至
翻折至![]() ,设直线
,设直线![]() 与直线
与直线![]() 所成角为α,直线
所成角为α,直线![]() 与平面
与平面![]() 所成角为β,二面角
所成角为β,二面角![]() 的平面角为γ,当γ为锐角时( )
的平面角为γ,当γ为锐角时( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据几何体的对称性将二面角![]() 的平面角等价于二面角
的平面角等价于二面角![]() 的平面角, 直线
的平面角, 直线![]() 与直线
与直线![]() 所成角等价于直线
所成角等价于直线![]() 与直线
与直线![]() 所成角;过点
所成角;过点![]() 做垂线,分别找到
做垂线,分别找到![]() ,根据直角三角形中边的大小关系,结合利用其正弦余弦值,即可比较其大小.
,根据直角三角形中边的大小关系,结合利用其正弦余弦值,即可比较其大小.
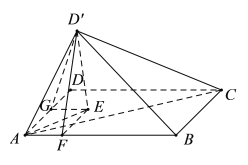
根据几何体的对称性知道二面角![]() 的平面角等于二面角
的平面角等于二面角![]() 的平面角.
的平面角.
作![]() 平面
平面![]() 于点
于点![]() ,则
,则![]() .
.
作![]() 于点
于点![]() ,连接
,连接![]() .
.
由于![]() ,则
,则![]() 平面
平面![]() .
.
故![]() ,则
,则![]() 即为二面角
即为二面角![]() 的平面角,
的平面角,
即![]() .
.
由于![]() 平面
平面![]() ,则
,则![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角.
所成角.
即![]() .
.
由于![]() ,则
,则![]() ,
,
而![]() ,
,![]() ,则
,则![]() ,
,
又因为![]() 为锐角,即
为锐角,即![]() .
.
由于四边形![]() 为矩形,则
为矩形,则![]()
![]()
![]() ,
,
故直线![]() 与直线
与直线![]() 所成角等于直线
所成角等于直线![]() 与直线
与直线![]() 等于所成角,
等于所成角,
即![]() .
.
作![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,而
,而![]() ,
,
则四边形![]() 为矩形,则
为矩形,则![]() .
.
在![]() 中,
中,![]() ; 在
; 在![]() 中,
中,![]() .
.
而![]() ,则
,则![]() ,
,
又因![]() 为锐角,所以
为锐角,所以![]() .
.
故![]() .
.
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.
”表示乙村贫困户.
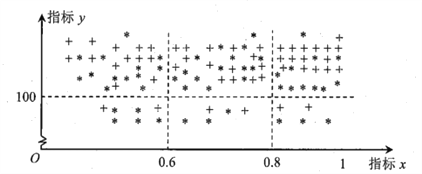
若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;
,则认定该户为“低收入户”;
若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
(1)从甲村50户中随机选出一户,求该户为“今年不能脱贫的绝对贫困户”的概率;
(2)若从所有“今年不能脱贫的非绝对贫困户”中选3户,用![]() 表示所选3户中乙村的户数,求
表示所选3户中乙村的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2012年12月18日,作为全国首批开展空气质量新标准监测的74个城市之一,郑州市正式发布![]() 数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(
数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(![]() ),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的
),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的![]() 的平均值为依据,播报我市的空气质量.
的平均值为依据,播报我市的空气质量.
(Ⅰ)若某日播报的![]() 为118,已知轻度污染区
为118,已知轻度污染区![]() 的平均值为74,中度污染区
的平均值为74,中度污染区![]() 的平均值为114,求重度污染区
的平均值为114,求重度污染区![]() 的平均值;
的平均值;
(Ⅱ)如图是2018年11月的30天中![]() 的分布,11月份仅有一天
的分布,11月份仅有一天![]() 在
在![]() 内.
内.
组数 | 分组 | 天数 |
第一组 |
| 3 |
第二组 |
| 4 |
第三组 |
| 4 |
第四组 |
| 6 |
第五组 |
| 5 |
第六组 |
| 4 |
第七组 |
| 3 |
第八组 |
| 1 |
①郑州市某中学利用每周日的时间进行社会实践活动,以公布的![]() 为标准,如果
为标准,如果![]() 小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
②在“创建文明城市”活动中,验收小组把郑州市的空气质量作为一个评价指标,从当月的空气质量监测数据中抽取3天的数据进行评价,设抽取到![]() 不小于180的天数为
不小于180的天数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《 环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过
的年平均浓度不得超过![]() 微克/立方米,
微克/立方米,![]() 的
的![]() 小时平均浓度不得超过
小时平均浓度不得超过![]() 微克/立方米.我市环保局随机抽取了一居民区
微克/立方米.我市环保局随机抽取了一居民区![]() 年
年![]() 天
天![]() 的
的![]() 小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
组别 |
| 频数(天) | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
(1)这![]() 天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.
天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.

①求图中![]() 的值;
的值;
②求样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
(2)将频率视为概率,对于![]() 年的某
年的某![]() 天,记这
天,记这![]() 天中该居民区
天中该居民区![]() 的
的![]() 小时平均浓度符合环境空气质量标准的天数为
小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,AD⊥PD,点F为棱PD的中点.
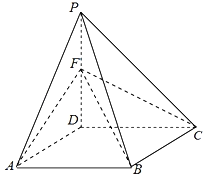
(1)在棱BC上是否存在一点E,使得CF∥平面PAE,并说明理由;
(2)若AC⊥PB,二面角D﹣FC﹣B的余弦值为![]() 时,求直线AF与平面BCF所成的角的正弦值.
时,求直线AF与平面BCF所成的角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com