
【题目】如图,平面四边形ABCD中,E、F是AD、BD中点,AB=AD=CD=2, BD=2![]() ,∠BDC=90°,将△ABD沿对角线BD折起至△
,∠BDC=90°,将△ABD沿对角线BD折起至△![]() ,使平面
,使平面![]() ⊥平面BCD,则四面体
⊥平面BCD,则四面体![]() 中,下列结论不正确是 ( )
中,下列结论不正确是 ( )
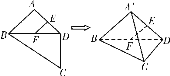
A. EF∥平面![]()
B. 异面直线CD与![]() 所成的角为90°
所成的角为90°
C. 异面直线EF与![]() 所成的角为60°
所成的角为60°
D. 直线![]() 与平面BCD所成的角为30°
与平面BCD所成的角为30°
【答案】C
【解析】
根据线线平行判定定理、异面直线所成角、直线与平面所成角等知识对选项A、B、C、D进行逐一判断其正确与否.
解:选项A:因为E、F是AD、BD中点,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以EF∥平面![]() ,
,
所以选项A正确;
选项B:因为平面![]() ⊥平面BCD,
⊥平面BCD,
平面![]()
![]() 平面BCD
平面BCD![]() ,
,
且∠BDC=90°,即![]() ,
,
又因为![]() 平面BCD,
平面BCD,
故![]() 平面
平面![]() ,
,
故![]()
![]() ,
,
所以异面直线CD与![]() 所成的角为90°,
所成的角为90°,
选项B正确;
选项C:由选项B可知![]() 平面
平面![]() ,
,
所以![]()
![]() ,
,
因为AD=CD=2,
即![]() =CD=2,
=CD=2,
所以由勾股定理得,![]() ,
,
在![]() 中,
中,
BC=![]() ,
,
在![]() 中,
中,
![]() ,
,
故![]() ,即
,即![]() ,
,
因为![]() ,
,
所以![]() ,
,
故选项C错误;
选项D:连接![]()
因为![]()
所以![]()
因为![]() 是中点,
是中点,
所以![]() ,
,
因为平面![]() ⊥平面BCD,
⊥平面BCD,
平面![]()
![]() 平面BCD
平面BCD![]() ,
,
又因为![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() ,
,
所以![]() 即为直线
即为直线![]() 与平面BCD所成的角,
与平面BCD所成的角,
在![]() 中,
中,![]() ,
,![]() ,
,
所以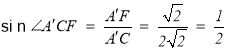 ,
,
所以![]() ,
,
故直线![]() 与平面BCD所成的角为30°,
与平面BCD所成的角为30°,
故选项D正确,
本题不正确的选项为C,故选C.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣x+1.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程:
(2)若非零实数a使得f(x)![]() ax
ax![]() ax2
ax2![]() 对x∈[1,+∞)恒成立,求a的取值范围.
对x∈[1,+∞)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某共享单车经营企业欲向甲市投放单车,为制定适宜的经营策略,该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段,A,B两个调查小组分赴全市不同区域发放问卷并及时收回;在整理分析阶段,两个调查小组从所获取的有效问卷中,针对15至45岁的人群,按比例随机抽取了300份,进行了数据统计,具体情况如下表:
组别 年龄 | A组统计结果 | B组统计结果 | ||
经常使用单车 | 偶尔使用单车 | 经常使用单车 | 偶尔使用单车 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本,再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.求这60人中“年龄达到35岁且偶尔使用单车”的人数;
(2)从统计数据可直观得出“是否经常使用共享单车与年龄(记作![]() 岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄
岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄![]() 应取25还是35?请通过比较
应取25还是35?请通过比较![]() 的观测值的大小加以说明.
的观测值的大小加以说明.
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我边防局接到情报,在海礁![]() 所在直线
所在直线![]() 的一侧点
的一侧点![]() 处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕:如图,已知快艇出发位置在
处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕:如图,已知快艇出发位置在![]() 的另一侧码头
的另一侧码头![]() 处,
处,![]() 公里,
公里,![]() 公里,
公里,![]() ;
;

(1)是否存在点![]() ,使快艇沿航线
,使快艇沿航线![]() 或
或![]() 的路程相等;如存在,则建立适当的直角坐标系,求出点
的路程相等;如存在,则建立适当的直角坐标系,求出点![]() 的轨迹方程,且画出轨迹的大致图形;如不存在,请说明理由;
的轨迹方程,且画出轨迹的大致图形;如不存在,请说明理由;
(2)问走私船在怎样的区域上时,路线![]() 比路线
比路线![]() 的路程短,请说明理由.
的路程短,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线l经过椭圆
的准线l经过椭圆![]() 的左焦点,且l与椭圆交于A,B两点,过椭圆N右焦点
的左焦点,且l与椭圆交于A,B两点,过椭圆N右焦点![]() 的直线交抛物线M于C,D两点,交椭圆于G,H两点,且
的直线交抛物线M于C,D两点,交椭圆于G,H两点,且![]() 面积为3.
面积为3.
(1)求椭圆N的方程;
(2)当![]() 时,求
时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆市第八中学校为了解学生喜爱运动是否与性别有关,从全校学生中随机抽取50名学生进行问卷调查,得到如图所示的![]() 列联表.
列联表.
喜爱运动 | 不喜爱运动 | 合计 | |
男生 | 22 | 8 | 30 |
女生 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
附: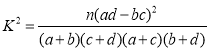 ,
,![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)能否有97.5%以上的把握认为“喜爱运动”与“性别”有关;
(2)用分层抽样的方法从被调查的20名女生中抽取5名进行问卷调查,求抽取喜爱运动的女生、不喜爱运动的女生各有多少的人;
(3)在(2)抽取的女生中,随机选出2人进行座谈,求至少有1名是喜爱运动的女生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“斗拱”是中国古代建筑中特有的构件,从最初的承重作用,到明清时期集承重与装饰作用于一体。在立柱顶、额枋和檐檩间或构架间,从枋上加的一层层探出成弓形的承重结构叫拱,拱与拱之间垫的方形木块叫斗。如图所示,是“散斗”(又名“三才升”)的三视图,则它的体积为( )

A. ![]() B.
B. ![]() C. 53 D.
C. 53 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的焦点和上项点分别为
的焦点和上项点分别为![]() ,我们称
,我们称![]() 为椭圆
为椭圆![]() 的“特征三角形”.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 若椭圆
的“特征三角形”.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 若椭圆![]() ,直线
,直线![]()
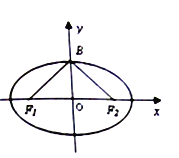
![]() 已知椭圆
已知椭圆![]() 与椭圆
与椭圆![]() 是相似椭圆,求
是相似椭圆,求![]() 的值及椭圆
的值及椭圆![]() 与椭圆
与椭圆![]() 相似比;
相似比;
![]() 求点
求点![]() 到椭圆
到椭圆![]() 上点的最大距离;
上点的最大距离;
![]() 如图,设直线
如图,设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() 两点,求证:
两点,求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com