小王、小李两位同学玩掷骰子(骰子质地均匀)游戏,规则:小王先掷一枚骰子,向上的点数记为x;小李后掷一枚骰子,向上的点数记为y.
(1)在直角坐标系xOy中,以(x,y)为坐标的点共有几个?求点(x,y)落在直线x+y=7上的概率;
(2)规定:若x+y≥10,则小王赢,若x+y≤4,则小李赢,其他情况不分输赢.试问这个规定公平吗?请说明理由.
解:(1)由题意知本题是一个古典概型,∵试验发生包含的事件是先后掷两次骰子,共有6×6=36种结果,
满足条件的事件是(x,y)为坐标的点落在直线2x+y=8上,
当x=1,y=6; x=2,y=5; x=3,y=4,x=4,y=3;x=5,y=2;x=6,y=1,共有6种结果,
∴根据古典概型的概率公式得到P=
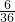
=

.
(2)∵若x+y≥10,则小王赢,若x+y≤4,则小李赢,其他情况不分输赢.
而满足x+y≥10的(x,y)共有(4,6)、(6,4)、(5,6)、(6,5)、(6,6)、(5,5)6种情况.
满足x+y≤4的(x,y)共有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)6种情况.
故小王和小李赢的概率相等,都等于
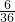
=

,故这个规定公平.
分析:(1)所有的结果共有6×6种结果,满足条件的事件是(x,y)为坐标的点落在直线x+y=7上,列举当x=1,y=6;x=2,y=5;x=3,y=4; x=4,y=3;x=5,y=2;x=6,y=1,
共有6种结果,由此得到所求的概率.
(2)用列举法分别求得小王和小李赢的基本事件的个数,求得小王和小李赢的概率相等,从而得到这个规定公平.
点评:本题考查古典概型的概率公式,考查满足直线方程的点,考查利用列举法得到事件数,本题是一个基础题,适合文科学生做,列举时注意要以x为主来讨论,属于基础题.

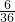 =
= .
.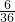 =
= ,故这个规定公平.
,故这个规定公平.

 阅读快车系列答案
阅读快车系列答案