
����Ŀ��ijУ�����ȡij�θ�����ѧģ�⿼�Լס��������10��ͬѧ�Ŀ���ɼ�������60�֣���ͳ�ƺ��óɼ����ݵľ�Ҷͼ����ʮλ����Ϊ������λ����ΪҶ������ͼ��ʾ�� ���ֱ�����������ݵ�ƽ���������Ƚ��ĸ��༶�Ŀ���ƽ���ɼ����ã�
�������������ݸ�ȡ�������ݣ�������������2�����֣�60�֣��ĸ��ʣ�
���涨����ɼ�������55��Ϊ������۾���������20�˵��������������ƴ˴θ�����ѧģ����������ݣ�������������ѡ4�ˣ���X��ʾ�鵽������۾�����ѧ����������X�ķֲ��м���ѧ������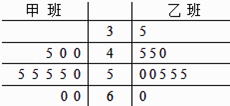
���𰸡��⣺��I���ס����������ݵ�ƽ�����ֱ�Ϊ51.5��49�� �װ�Ŀ���ƽ���ɼ����ã�
��II��������������ݸ�ȡ�������ݣ�������2�����֣�60�֣�Ϊ�¼�A��
��P��A��= ![]() =
= ![]() ��
��
��III�� ![]()
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
![]() ���ˣ�
���ˣ�
����������I���������ݼ����������ݵ�ƽ���������������������зֱ��ȡһ�����ݣ�������������2�����֣�60�֣��ĸ��ʣ����� ![]() ���������ʣ��ɵ�X�ķֲ��м���ѧ������
���������ʣ��ɵ�X�ķֲ��м���ѧ������
�����㾫����������ɢ�������������ֲ��ж���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪���������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() ��a��b��0�������ҽ���ֱ�ΪF1��F2 �� ������e=
��a��b��0�������ҽ���ֱ�ΪF1��F2 �� ������e= ![]() ����˫����
����˫���� ![]() ����ͬ�Ľ��㣮 ��I������ԲC�ı����̣�
����ͬ�Ľ��㣮 ��I������ԲC�ı����̣�
��II������F1��ֱ��l�����ԲC����M��N���㣬��| ![]() +
+ ![]() N|=
N|= ![]() ����ֱ��l�ķ��̣�
����ֱ��l�ķ��̣�
�����Ƿ����Բ����ԭ���Բ��ʹ�ø�Բ����һ����������ԲC����������A��B����OA��OB�������ڣ�д����Բ�ķ��̣�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�У�����ABCDΪƽ���ı��Σ���DAB=60�㣬AB=2AD��PD�͵���ABCD�� ����֤����PA��BD��
������PD=AD��������A��PB��C������ֵ��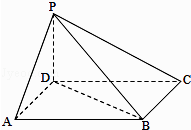
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() չ��ʽ�У�������Ķ���ʽϵ���������Ķ���ʽϵ���ı���14��3��
չ��ʽ�У�������Ķ���ʽϵ���������Ķ���ʽϵ���ı���14��3��
��1����n��
��2����x2���ϵ����
��3����չ��ʽ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
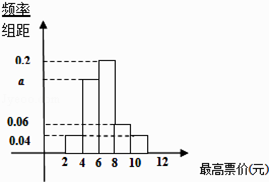
����Ŀ��2014��5�£���������������ֶμƼ۵�����������ԡ����ܽ��ܵ����Ʊ���Ƕ��٣���������⣬��ij����վ�������50�˽��е��飬�������ݵ�Ƶ�ʷֲ�ֱ��ͼ������������35�����µ�������ͳ�ƽ�����£� ������Ƶ�ʷֲ�ֱ��ͼ����a��ֵ��������������˵����������ʵ�����壻
���ӡ��ܽ��ܵ����Ʊ�ۡ�����[8��10����[10��12]�ı��������и����ѡȡ3�˽����ٵ��飬��ѡ�е�6����35�����ϣ���35�꣩������ΪX�����������X�ķֲ��м���ѧ������
���Ʊ�� | 35���������� |
[2��4�� | 2 |
[4��6�� | 8 |
[6��8�� | 12 |
[8��10�� | 5 |
[10��12] | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������彡��������ɱ�֣�������������������ij����ʵ��������������������������ҿ���������ʵ�鷢�֣����ڽ����ͷ������Ĺ����У������������ĺ���Ũ��y��mg/m3����ʱ��t��h�������ȣ��ͷ���Ϻ�y��t�ĺ�����ϵΪy=�� ![]() ��t��a��aΪ����������ͼ����֪�����ҵĿ����к���Ũ����0.25mg/m3����ʱ���������ʺ�����������ͼ����Ϣ����һ���ͷ�������ʼ����������h���ʺ�������
��t��a��aΪ����������ͼ����֪�����ҵĿ����к���Ũ����0.25mg/m3����ʱ���������ʺ�����������ͼ����Ϣ����һ���ͷ�������ʼ����������h���ʺ������� 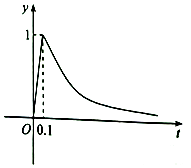
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ԲC�� ![]() +
+ ![]() =1��a��b��0������ԲC1��x2+y2=a2+b2Ϊ��ԲC�ġ�����Բ������֪��ԲC��������Ϊ
=1��a��b��0������ԲC1��x2+y2=a2+b2Ϊ��ԲC�ġ�����Բ������֪��ԲC��������Ϊ ![]() ���Ҿ����㣨0��1����
���Ҿ����㣨0��1����
��1����ʵ��a��b��ֵ��
��2��������P��0��m����m��0����ֱ��l����ԲC����ֻ��һ�������㣬��l����ԲC�İ���ԲC1���صõ��ҳ�Ϊ2 ![]() ����ʵ��m��ֵ��
����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȷ���� ��
�ٳ������м��ǵȲ�����Ҳ�ǵȱ����У�
���ڡ�ABC�У���sin2A+sin2B=sin2C�����ABCΪֱ�������Σ�
����A��BΪ��������ε������ڽǣ���tanAtanB��1��
����SnΪ����{an}��ǰn��ͣ�������е�ͨ��an=Sn��Sn��1��n��1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABCD�У�����ABCD�������Σ�����PD�͵���ABCD��PD=DC��E��PC���е㣬��E����EF��PB��PB�ڵ�F����֤�� 
��1��PA��ƽ��DEB��
��2��PB��ƽ��DEF��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com