Question

【题目】已知函数f（x）=lg（ ）为奇函数．
（1）求m的值，并求f（x）的定义域；
（2）判断函数f（x）的单调性，并证明；
（3）若对于任意θ∈[0， ]，是否存在实数λ，使得不等式f（cos2θ+λsinθ﹣ ）﹣lg3＞0．若存在，求出实数λ的取值范围；若不存在，请说明理由．

Answer 1

【答案】
（1）解：∵函数f（x）=lg（ ）为奇函数，

∴f（﹣x）=﹣f（x）在定义域内恒成立，

即lg（ ）=﹣lg（ ），

即lg（ ）+lg（ ）=0，

则 =1，即1﹣m2x2=1﹣x2，在定义域内恒成立，

∴m=﹣1或m=1，当m=1时，f（x）=lg（ ）=lg1=0，

∴m=﹣1，此时f（x）=lg ，

由 ＞0，解得﹣1＜x＜1，

故函数的定义域是（﹣1，1）

（2）解：∵f（x）=lg ，﹣1＜x＜1，任取﹣1＜x1＜x2＜1，

设u（x）= ，﹣1＜x＜1，

则u（x1）﹣u（x2）=

∵﹣1＜x1＜x2＜1，∴u（x1）﹣u（x2）＜0，∴u（x1）＜u（x2），即lgu（x1）＜lgu（x2），

∴f（x1）＜f（x2），即f（x）在定义域内单调递增

（3）解：假设存在实数λ，使得不等式不等式f（cos2θ+λsinθ﹣ ）﹣lg3＞0成立，

即不等式f（cos2θ+λsinθ﹣ ）＞lg3=f（ ），

由（1），（2）知： ＜cos2θ+λsinθ﹣ ＜1 对于任意θ∈[0， ]，

即 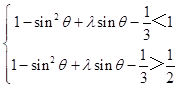，当θ=0时成立；

当θ∈（0， ]时，令sinθ=t，则 ，

即 ，则

【解析】（1）根据函数奇偶性的条件建立方程关系，即可求m的值，（2）根据函数单调性的定义即可判断函数f（x）的单调性；（3）利用三角函数姜不等式进行转化，解三角不等式即可得到结论．