
【题目】已知抛物线E:x2=2py(p>0)的焦点为F,点M是直线y=x与抛物线E在第一象限内的交点,且|MF|=5.
(1)求抛物E的方程.
(2)直线l与抛物线E相交于两点A,B,过点A,B分别作AA1⊥x轴于A1,BB1⊥x轴于B1,原点O到直线l的距离为1.求![]() 的最大值.
的最大值.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 是双曲线
是双曲线![]() :
:![]() 的左右焦点,其渐近线为
的左右焦点,其渐近线为![]() ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3.
(1)求双曲线![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 的法向量为
的法向量为![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若双曲线![]() 在第四象限的部分存在一点
在第四象限的部分存在一点![]() 满足
满足![]() ,求
,求![]() 的值及
的值及![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() 左,右顶点分别为
左,右顶点分别为![]() ,
,![]() ,点
,点![]() ,
,![]() ,为椭圆
,为椭圆![]() 上位于
上位于![]() 轴上方的两点,且
轴上方的两点,且![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记直线
,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查消费者的维权意识,青岛二中的学生记者在五四广场随机调查了120名市民,按他们的年龄分组:第1组[20.30),第2组[30,40),第3组[40,50),第4组[50,60),第5组[60,70),得到的频率分布直方图如图所示.
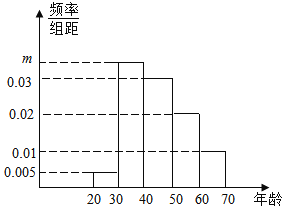
(1)若要从被调查的市民中选1人采访,求被采访人恰好在第2组或第5组的概率;
(2)已知第1组市民中男性有2人,学生要从第1组中随机抽取3名市民组成维权志愿者服务队,求至少有两名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于实数![]() 和两定点
和两定点![]() ,在某图形上恰有
,在某图形上恰有![]() 个不同的点
个不同的点![]() ,使得
,使得![]() ,称该图形满足“
,称该图形满足“![]() 度契合”.若边长为4的正方形
度契合”.若边长为4的正方形![]() 中,
中,![]() ,且该正方形满足“4度契合”,则实数
,且该正方形满足“4度契合”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 中点现将四边形
中点现将四边形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,得到如图②所示的多面体在图②中,
,得到如图②所示的多面体在图②中,
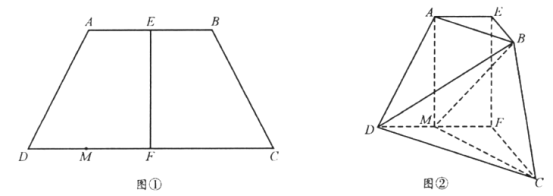
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海湿地如图所示,A、B和C、D分别是以点O为中心在东西方向和南北方向设置的四个观测点,它们到点O的距离均为![]() 公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
公里,实线PQST是一条观光长廊,其中,PQ段上的任意一点到观测点C的距离比到观测点D的距离都多8公里,QS段上的任意一点到中心点O的距离都相等,ST段上的任意一点到观测点A的距离比到观测点B的距离都多8公里,以O为原点,AB所在直线为x轴建立平面直角坐标系xOy.
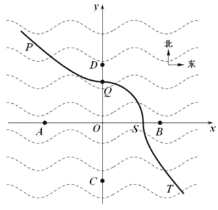
(1)求观光长廊PQST所在的曲线的方程;
(2)在观光长廊的PQ段上,需建一服务站M,使其到观测点A的距离最近,问如何设置服务站M的位置?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinπx,g(x)=x2﹣x+2,则( )
A. 曲线y=f(x)+g(x)不是轴对称图形
B. 曲线y=f(x)﹣g(x)是中心对称图形
C. 函数y=f(x)g(x)是周期函数
D. 函数![]() 最大值为
最大值为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com