
【题目】坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,又在直角坐标系
,又在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (t为参数).
(t为参数).
(1)求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() 在曲线
在曲线![]() 上,点Q在曲线
上,点Q在曲线![]() 上,若
上,若![]() 的最小值为
的最小值为![]() ,求此时点
,求此时点![]() 的直角坐标.
的直角坐标.
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
的大小是60°,连接![]() ,如图:
,如图:
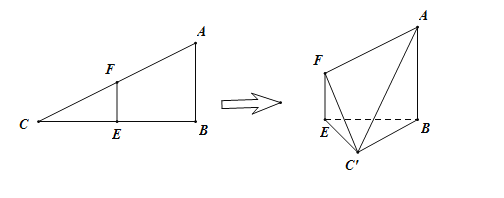
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记![]() 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,![]() 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.
(Ⅰ)求![]() 的分布列;
的分布列;
(Ⅱ)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,过点
中,过点![]() 作倾斜角为
作倾斜角为![]() 的直线
的直线![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 上各点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线
上各点的横坐标伸长为原来的2倍,纵坐标不变,得到曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() .
.
(1)求直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AB//CD,AB=3,CD=6,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=3,将梯形ABCD沿AE,BF同侧折起,使得平面ADE⊥平面ABFE,平面ADE∥平面BCF,得到图2.
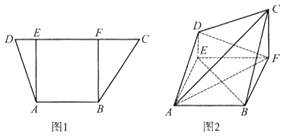
(1)证明:BE//平面ACD;
(2)求三棱锥C﹣AED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年1月1日全面实施二孩政策以来,为了了解生二孩意愿与年龄段是否有关,某市选取“75后”和“80后”两个年龄段的已婚妇女作为调查对象,进行了问卷调查,共调查了40名“80后”,40名“75后”,其中调查的“80后”有10名不愿意生二孩,其余的全部愿意生二孩;调查的“75后”有5人不愿意生二孩,其余的全部愿意生二孩.
(1)根据以上数据完成下列![]() 列联表;
列联表;
年龄段 | 不愿意 | 愿意 | 合计 |
“80后” | |||
“75后” | |||
合计 |
(2)根据![]() 列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
参考公式: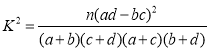 (其中
(其中![]() )
)
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P-ABC(如图一)的平面展开图(如图二)中,四边形ABCD为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥P-ABC中:
均为正三角形,在三棱锥P-ABC中:
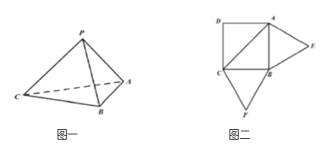
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上运动,当直线BM与平面PAC所成的角最大时,求直线MA与平面MBC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com