
【题目】已知数列{an}满足(an+1﹣1)(an﹣1)=3(an﹣an+1),a1=2,令bn= ![]() .
.
(1)求数列{bn}的通项公式;
(2)求数列{bn3n}的前n项和Sn .
【答案】
(1)解:∵(an+1﹣1)(an﹣1)=3(an﹣an+1)=3[(an﹣1)﹣(an+1﹣1)],
∴ ![]() =
= ![]() ,即bn+1﹣bn=
,即bn+1﹣bn= ![]() .
.
∴数列{bn}是等差数列,首项为1,公差为 ![]() .
.
∴bn=1+ ![]() (n﹣1)=
(n﹣1)= ![]()
(2)解: ![]() =(n+2)3n﹣1.
=(n+2)3n﹣1.
∴数列{bn3n}的前n项和Sn=3+4×3+5×32+…+(n+2)3n﹣1.
∴3Sn=3×3+4×32+…+(n+1)×3n﹣1+(n+2)3n,
∴﹣2Sn=3+3+32+…+3n﹣1﹣+(n+2)3n=2+ ![]() ﹣(n+2)3n=2+
﹣(n+2)3n=2+ ![]() ,
,
∴Sn= ![]()
【解析】(1)由(an+1﹣1)(an﹣1)=3(an﹣an+1)=3[(an﹣1)﹣(an+1﹣1)],可得 ![]() =
= ![]() ,即bn+1﹣bn=
,即bn+1﹣bn= ![]() .利用等差数列的通项公式即可得出.(2)
.利用等差数列的通项公式即可得出.(2) ![]() =(n+2)3n﹣1 . 利用“错位相减法”与等比数列的前n项和公式即可得出.
=(n+2)3n﹣1 . 利用“错位相减法”与等比数列的前n项和公式即可得出.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() 表示焦点在x轴上的椭圆,命题q:方程(k﹣1)x2+(k﹣3)y2=1表示双曲线.若p∨q为真,p∧q为假,求实数k的取值范围.
表示焦点在x轴上的椭圆,命题q:方程(k﹣1)x2+(k﹣3)y2=1表示双曲线.若p∨q为真,p∧q为假,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC的顶点A(5,1),B(1,5).
(1)若A为直角△ABC的直角顶点,且顶点C在y轴上,求BC边所在直线方程;
(2)若等腰△ABC的底边为BC,且C为直线l:y=2x+3上一点,求点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 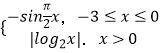 ,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+
,若方程f(x)=a有四个不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则x3(x1+x2)+ ![]() 的取值范围为( )
的取值范围为( )
A.(﹣1,+∞)
B.(﹣1,1)
C.(﹣∞,1)
D.[﹣1,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间D上的函数f(x),如果满足:对任意x∈D,都存在常数M≥0,有|f(x)|≤M,则称f(x)是区间D上有界函数,其中M称为f(x)上的一个上界,已知函数g(x)=log ![]() 为奇函数.
为奇函数.
(1)求函数g(x)在区间[ ![]() ,
, ![]() ]上的所有上界构成的集合;
]上的所有上界构成的集合;
(2)若g(1﹣m)+g(1﹣m2)<0,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0(a>0),命题q:实数x满足 ![]() ≤0。
≤0。
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且DE=2PE.
(Ⅰ)求异面直线PA与CD所成的角的大小;
(Ⅱ)求证:BE⊥平面PCD;
(Ⅲ)求二面角A﹣PD﹣B的大小.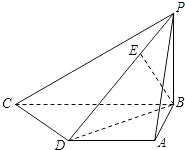
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com