
(1)求a1,a3;
(2)猜想an的表达式,并用数学归纳法加以证明;
(3)求证:以(an,![]() )为坐标的点Pn(n=1,2,…)都落在同一直线上.
)为坐标的点Pn(n=1,2,…)都落在同一直线上.
(1)解:由已知得Sn=![]() ×n,?
×n,?
当n=1时,S1=a1,?
∴2a1=a1+a.?
∴a1=a.?
当n=3时,S3=a1+a2+a3,?
∴2(a1+a2+a3)=3(a3+a).?
∴2(a+a+2+a3)=3(a3+a).?
∴a3=a+4.
(2)解:由a1=a,a2=a+2,a3=a+4,…,猜想an=a+2(n-1),
证明:①当n=1时,左边=a1=a,右边=a+2(1-1)=a,
∴当n=1时,等式成立.当n=2时,左边=a2=a+2,?
右边=a+2(2-1)=a+2,?
∴当n=2时,等式成立.?
②假设n=k(k∈N*,k≥2)时,等式成立,即ak=a+2(k-1)?,?
则当n=k+1时,ak+1=Sk+1-Sk=![]() (k+1)-
(k+1)-![]() k,?
k,?
∴2ak+1=(ak+1+a)(k+1)-(ak+a)k.?
∴(k-1)ak+1=kak-a.?
∵k≥2,?
∴ak+1=![]() ak-
ak-![]() .?
.?
将ak=a+2(k-1)代入,得?
ak+1=![]() [a+2(k-1)]-
[a+2(k-1)]-![]()
=![]() =a+2[(k+1)-1].?
=a+2[(k+1)-1].?
∴当n=k+1时,等式也成立.由①②可知,对任何正整数n,等式an=a+2(n-1)都成立.
(3)证明:当n≥2时,an=a+2(n-1),?
∴Sn=![]() ×n=
×n=![]() ×n=(a+n-1)n.?
×n=(a+n-1)n.?
∴![]() =a+n-1.?
=a+n-1.?
∴(![]() -1)-(
-1)-(![]() -1)=n-1.?
-1)=n-1.?
又an-a1=2(n-1),?
∴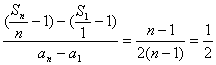 .
.
∴点Pn(n=1,2,3,…)都落在同一直线上.
温馨提示
用递推公式求出数列的前几项并归纳猜想其通项公式或猜想相关结论,再用数学归纳法证明之,这是数学归纳法的重要应用.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
| n+1 |
| 2 |
| 2n |
| an |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com