
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,且过点M(4,1). (Ⅰ)求椭圆C的方程;
,且过点M(4,1). (Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=x+m(m≠﹣3)与椭圆C交于P,Q两点,记直线MP,MQ的斜率分别为k1 , k2 , 试探究k1+k2是否为定值.若是,请求出该定值;若不是,请说明理由.
【答案】解:(Ⅰ)依题意,e= ![]() =
= ![]() =
= ![]() ,则a2=4b2 , 由椭圆过点M(4,1),代入椭圆方程:
,则a2=4b2 , 由椭圆过点M(4,1),代入椭圆方程: ![]() ,解得:b2=5,a2=20,
,解得:b2=5,a2=20,
∴椭圆的标准方程: ![]() ;
;
(Ⅱ)k1+k2为定值0,下面给出证明,
设P(x1 , y1),P(x2 , y2),
则 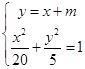 ,整理得:5x2+8mx+2m2﹣20=0,
,整理得:5x2+8mx+2m2﹣20=0,
△=(8m)2﹣4×5×(2m2﹣20)>0,解得:﹣5<m<5,且m≠﹣3,
则x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
则k1+k2= ![]() +
+ ![]() =
= ![]() ,
,
则(y1﹣1)(x2﹣4)+(y2﹣1)(x1﹣4)=(x1+m﹣1)(x2﹣4)+(x2+m﹣1)(x1﹣4),
=2x1x2+(m﹣5)(x1+x2)﹣8(m﹣1),
=2× ![]() +(m﹣5)(﹣
+(m﹣5)(﹣ ![]() )﹣8(m﹣1),
)﹣8(m﹣1),
=0,
∴k1+k2=0,
∴k1+k2为定值0
【解析】(Ⅰ)由椭圆的离心率公式,求得a2=4b2 , 将M代入椭圆方程,即可求得a和b的值,求得椭圆方程;(Ⅱ)将直线l:代入椭圆方程,利用韦达定理及直线的斜率公式,即可取得k1+k2=0.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查50人,并将调查情况进行整理后制成如表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,60) |
频数 | 10 | 10 | 10 | 10 | 10 |
赞成人数 | 3 | 5 | 6 | 7 | 9 |
(1)世界联合国卫生组织规定:[15,45)岁为青年,(45,60)为中年,根据以上统计数据填写以下2×2列联表:
青年人 | 中年人 | 合计 | |
不赞成 |
|
|
|
赞成 |
|
|
|
合计 |
|
|
|
(2)判断能否在犯错误的概率不超过0.05的前提下,认为赞成“车柄限行”与年龄有关? 附: ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
独立检验临界值表:
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
(3)若从年龄[15,25),[25,35)的被调查中各随机选取1人进行调查,设选中的两人中持不赞成“车辆限行”态度的人员为ξ,求随机变量ξ的分布列和数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知边长为2的菱形ABCD中,∠BCD=60°,E为DC的中点,如图1所示,将△BCE沿BE折起到△BPE的位置,且平面BPE⊥平面ABED,如图2所示. 
(Ⅰ)求证:△PAB为直角三角形;
(Ⅱ)求二面角A﹣PD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面ABCD是平行四边形,△PAB与△ABC是等腰三角形,PA⊥平面ABCD,PA=2,AD=2 ![]() ,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上.
,AC⊥BA,点E是线段AB上靠近点B的一个三等分点,点F、G分别在线段PD,PC上. 
(Ⅰ)证明:CD⊥AG;
(Ⅱ)若三棱锥E﹣BCF的体积为 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|﹣|x+2|. (Ⅰ)求不等式﹣2<f(x)<0的解集A;
(Ⅱ)若m,n∈A,证明:|1﹣4mn|>2|m﹣n|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)的图象是以原点为圆心、1为半径的两段圆弧,如图所示.则不等式f(x)>f(-x)+x的解集为( )

A. ![]() ∪(0,1]
∪(0,1]
B. [-1,0)∪![]()
C. ![]() ∪
∪![]()
D. ![]() ∪
∪![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x3+x,x∈R,当 ![]() 时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
A.(0,1)
B.(﹣∞,0)
C.![]()
D.(﹣∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.

(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com