
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
分析 可作图,作向量$\overrightarrow{CD}=\frac{1}{6}\overrightarrow{CB},\overrightarrow{CE}=\frac{1}{3}\overrightarrow{CA}$,从而$\overrightarrow{CM}=\overrightarrow{CD}+\overrightarrow{CE}$,可设B到边AC的距离为d1,M到AC的距离为d2,d2也等于E到AC的距离,这样便可得出$\frac{{S}_{△MAC}}{{S}_{△ABC}}=\frac{1}{6}$,而同理可以得出$\frac{{S}_{△MBC}}{{S}_{△ABC}}=\frac{1}{3}$,从而便可得出S△MAC:S△MAB的值.
解答 解:如图,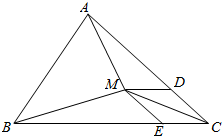
$\overrightarrow{CD}=\frac{1}{6}\overrightarrow{CB},\overrightarrow{CE}=\frac{1}{3}\overrightarrow{CA}$,则$\overrightarrow{CM}=\overrightarrow{CD}+\overrightarrow{CE}$;
令B到AC的距离为d1,M到AC的距离为d2,d2也是E到AC的距离,则$\frac{{{S_{△MAC}}}}{{{S_{△ABC}}}}=\frac{d_2}{d_1}=\frac{1}{6}$;
同理$\frac{{{S_{△MBC}}}}{{{S_{△ABC}}}}=\frac{1}{3}$;
∴$\frac{{S}_{△MAB}}{{S}_{△ABC}}=1-\frac{1}{6}-\frac{1}{3}=\frac{1}{2}$;
∴$\frac{{{S_{△MAC}}}}{{{S_{△MAB}}}}=\frac{1}{3}$.
故选A.
点评 考查向量数乘的几何意义,向量加法的平行四边形法则,相似三角形的比例关系,以及三角形的面积公式.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | 3l-2m+$\frac{1}{3}n$ | B. | 3l-2m-$\frac{1}{3}n$ | C. | 3l-2m+3n | D. | 3l-2m-3n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 数学成绩分组 | [50,60﹚ | [60,70﹚ | [70,80﹚ | [80,90﹚ | [90,100﹚ | [100,110﹚ | [110,120] |
| 频数 |

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{5}$,1) | B. | (-∞,-$\frac{1}{5}$)∪(1,+∞) | C. | [-$\frac{1}{5}$,1) | D. | (-∞,-$\frac{1}{5}$]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点P为体对角线的中点.若△PAC的正视图的最高点与侧视图的每一个顶点相连所得的几何体的体积为V1,正方体外接球的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点P为体对角线的中点.若△PAC的正视图的最高点与侧视图的每一个顶点相连所得的几何体的体积为V1,正方体外接球的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值为( )| A. | $\frac{1}{4π}$ | B. | $\frac{\sqrt{3}}{4π}$ | C. | $\frac{\sqrt{3}}{36π}$ | D. | $\frac{\sqrt{6}}{36π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 不喜欢英语 | 喜欢英语 | 总计 | |
| 男生 | 40 | 18 | 58 |
| 女生 | 15 | 27 | 42 |
| 总计 | 55 | 45 | 100 |
| p(K2≥k) | 0.100 | 0.050 | 0.025 | 0.01 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{25}$ | C. | $\frac{1}{15}$ | D. | $\frac{1}{30}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com