
【题目】已知函数![]()
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若关于![]() 的方程
的方程![]() 有三个不同的实根,求实数
有三个不同的实根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)12x﹣y﹣17=0(2)(﹣3,﹣2)
【解析】
(1)将x=2分别代入原函数解析式和导函数解析式,求出切点坐标和切线斜率,由点斜式可得曲线y=f(x)在点(2,f(2))处的切线方程;
(2)若关于x的方程f(x)+m=0有三个不同的实根,则﹣m值在函数两个极值之间,利用导数法求出函数的两个极值,可得答案.
解:(1)当x=2时,f(2)=7
故切点坐标为(2,7)
又∵f′(x)=6x2﹣6x.
∴f′(2)=12
即切线的斜率k=12
故曲线y=f(x)在点(2,f(2))处的切线方程为y﹣7=12(x﹣2)
即12x﹣y﹣17=0
(2)令f′(x)=6x2﹣6x=0,解得x=0或x=1
当x<0,或x>1时,f′(x)>0,此时函数为增函数,
当0<x<1时,f′(x)<0,此时函数为减函数,
故当x=0时,函数f(x)取极大值3,
当x=1时,函数f(x)取极小值2,
若关于x的方程f(x)+m=0有三个不同的实根,则2<﹣m<3,即﹣3<m<﹣2
故实数m的取值范围为(﹣3,﹣2)


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为![]() ,
,![]() ,
,![]() ,假设各盘比赛结果相互独立.
,假设各盘比赛结果相互独立.
(I)求红队至少两名队员获胜的概率;
(II)用![]() 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】p:关于x的方程![]() 无解,q:
无解,q:![]() (
(![]() )
)
(1)若![]() 时,“
时,“![]() ”为真命题,“
”为真命题,“![]() ”为假命题,求实数a的取值范围.
”为假命题,求实数a的取值范围.
(2)当命题“若p,则q”为真命题,“若q,则p”为假命题时,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的有( )个
(1). 残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高.
(2). 回归直线一定过样本中心![]() 。
。
(3). 两个模型中残差平方和越小的模型拟合的效果越好。
(4) .甲、乙两个模型的![]() 分别约为0.88和0.80,则模型乙的拟合效果更好.
分别约为0.88和0.80,则模型乙的拟合效果更好.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥VABCD中,底面ABCD是矩形,VD⊥平面ABCD,过AD的平面分别与VB,VC交于点M,N.
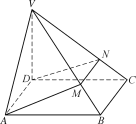
(1) 求证:BC⊥平面VCD;
(2) 求证:AD∥MN.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f![]() (x)g(x)+f(x)g
(x)g(x)+f(x)g![]() (x)<0且f(﹣1)=0则不等式f(x)g(x)<0的解集为( )
(x)<0且f(﹣1)=0则不等式f(x)g(x)<0的解集为( )
A.(﹣1,0)∪(1,+∞)B.(﹣1,0)∪(0,1)
C.(﹣∞,﹣1)∪(1,+∞)D.(﹣∞,﹣1)∪(0,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com