
【题目】下列函数中,在其定义域上既是偶函数又在(0,+∞)上单调递减的是( )
A.y=x2
B.y=x+1
C.y=﹣lg|x|
D.y=﹣2x
【答案】C
【解析】解:选项A:f(x)=x2的定义域为R,又∵f(﹣x)=(﹣x)2=x2 , ∴f(﹣x)=f(x),即f(x)是偶函数.但y=x2在(0,+∞)上单调递增,故A不正确;
选项B:记f(x)=x+1,则f(1)=2,f(﹣1)=0,∵f(﹣1)≠f(1),且f(﹣1)≠﹣f(1),∴y=x+1是非奇非偶函数,故B不正确;
选项C:定义域为(﹣∞,0)∪(0,+∞),记f(x)=﹣lg|x|,
∵f(﹣x)=﹣lg|﹣x|=﹣lg|x|,∴f(﹣x)=f(x),即f(x)是偶函数
当x∈(0,+∞)时,y=﹣lgx.∵y=lgx在(0,+∞)上单调递增,∴y=﹣lgx在(0,+∞)上单调递减故C正确;
选项D:记f(x)=﹣2x , 则f(1)=﹣ ![]() ,f(﹣1)=﹣2,∵f(﹣1)≠f(1),且f(﹣1)≠﹣f(1),∴y=﹣2x是非奇非偶函数,故D不正确.
,f(﹣1)=﹣2,∵f(﹣1)≠f(1),且f(﹣1)≠﹣f(1),∴y=﹣2x是非奇非偶函数,故D不正确.
故选:C.
【考点精析】认真审题,首先需要了解函数单调性的判断方法(单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较),还要掌握函数的奇偶性(偶函数的图象关于y轴对称;奇函数的图象关于原点对称)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段,垂足为
轴的垂线段,垂足为![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() ,当点
,当点![]() 在圆上运动时.
在圆上运动时.
(1)求点![]() 的轨迹
的轨迹![]() 的方程,并指出轨迹
的方程,并指出轨迹![]() .
.
(2)直线l不过原点O且不平行于坐标轴,l与C有两个交点A,B,线段AB的中点为M.证明:直线OM的斜率与直线l的斜率的乘积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆
是圆![]() :
: ![]() 上任意一点,点
上任意一点,点![]() 与圆心
与圆心![]() 关于原点对称.线段
关于原点对称.线段![]() 的中垂线与
的中垂线与![]() 交于
交于![]() 点.
点.
(1)求动点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)设点![]() ,若直线
,若直线![]() 轴且与曲线
轴且与曲线![]() 交于另一点
交于另一点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,证明:点
,证明:点![]() 恒在曲线
恒在曲线![]() 上,并求
上,并求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
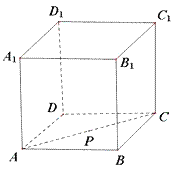
【题目】如图,在正方体ABCD﹣A1B1C1D1中,点P在面对角线AC上运动,给出下列四个命题:
①D1P∥平面A1BC1;
②D1P⊥BD;
③平面PDB1⊥平面A1BC1;
④三棱锥A1﹣BPC1的体积不变.
则其中所有正确的命题的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某海礁A处有一风暴中心,距离风暴中心A正东方向200km的B处有一艘轮船,正以北偏西a(a为锐角)角方向航行,速度为40km/h.已知距离风暴中心180km以内的水域受其影响.
(1)若轮船不被风暴影响,求角α的正切值的最大值?
(2)若轮船航行方向为北偏西45°,求轮船被风暴影响持续多少时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右顶点是双曲线
的左右顶点是双曲线![]() 的顶点,且椭圆
的顶点,且椭圆![]() 的上顶点到双曲线
的上顶点到双曲线![]() 的渐近线的距离为
的渐近线的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有如下3个命题;
①双曲线![]() 上任意一点
上任意一点![]() 到两条渐近线的距离乘积是定值;
到两条渐近线的距离乘积是定值;
②双曲线![]() 的离心率分别是
的离心率分别是![]() ,则
,则![]() 是定值;
是定值;
③过抛物线![]() 的顶点任作两条互相垂直的直线与抛物线的交点分别是
的顶点任作两条互相垂直的直线与抛物线的交点分别是![]() ,则直线
,则直线![]() 过定点;其中正确的命题有( )
过定点;其中正确的命题有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() (a>0,b>0)的渐近线方程为y=±
(a>0,b>0)的渐近线方程为y=±![]() x,O为坐标原点,点
x,O为坐标原点,点![]() 在双曲线上.
在双曲线上.
(I)求双曲线C的方程.
(II)若斜率为1的直线l与双曲线交于P,Q两点,且![]() =0,求直线l方程.
=0,求直线l方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2ωx(ω>0),将y=f(x)的图象向右平移 ![]() 个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
个单位长度后,若所得图象与原图象重合,则ω的最小值等于( )
A.2
B.4
C.6
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com