已知数列
的前
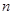项和为
，对于任意的
恒有
（1） 求数列
的通项公式
（2）若
证明：
科目：高中数学 来源： 题型：解答题
甲、乙两人用农药治虫，由于计算错误，在A、B两个喷雾器中分别配制
成12%和6%的药水各10千克，实际要求两个喷雾器中的农药的浓度是一样的，现在只有两个容量为1千
克的药瓶，他们从A、B两个喷雾器中分别取1千克的药水，将A中取得的倒入B中，B中取得的倒入A
中，这样操作进行了n次后，A喷雾器中药水的浓度为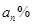
，B喷雾器中药水的浓度为
．
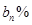（1）证明：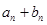
是一个常数；
（2）求
与
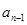的关系式；
（3）求的表达式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（2）关键是得到
时，
两式相减得：
得
，满足
数列
是以
为首项，2为公比的等比数列． 
,由
时,
则不等式成立.
,当
(用数学归纳法证明,略)
满足
，
，
，且
是等比数列。
的值；
；
…
}中，
，又
成等比数列.
，求数列{
}的前n项和
.
的前
项和为
，数列
是首项为
，公差为
的等差数列，且
成等比数列．
，求数列
的前
．
是等差数列，且
，
，
，求数列
前n项和
.
中，
，满足
。
为等差数列;
项和
.
中，
，求数列
的前n项和
.