
【题目】如图,在底面为正方形的四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,PA⊥AD,PA=AD,则异面直线PB与AC所成的角为( ) 
A.30°
B.45°
C.60°
D.90°
【答案】C
【解析】解:由题意:底面ABCD为正方形,PA⊥平面ABCD,
分别过P,D点作AD,AP的平行线交于M,连接CM,AM,
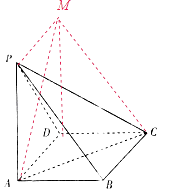
∵PM∥AD,AD∥BC,PM=AD,AD=BC.
∴PBCM是平行四边形,
∴PB∥CM,
所以∠ACM就是异面直线PB与AC所成的角.
设PA=AB=a,在三角形ACM中,AM= ![]() a,AC=
a,AC= ![]() a,CM=
a,CM= ![]() a
a
∴三角形ACM是等边三角形.
所以∠ACM等于60°,即异面直线PB与AC所成的角为60°.
故选:C
【考点精析】关于本题考查的异面直线及其所成的角和空间中直线与直线之间的位置关系,需要了解异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知定义在区间(﹣1,1)上的增函数f(x)= ![]() 为奇函数,且f(
为奇函数,且f( ![]() )=
)= ![]()
(1)求函数f(x)的解析式;
(2)解关于t的不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程  (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为:ρ=4cosθ.
(1)把直线l的参数方程化为极坐标方程,把曲线C的极坐标方程化为普通方程;
(2)求直线l与曲线C交点的极坐标(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是( ) 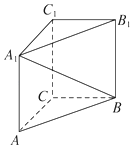
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某百货公司1~6月份的销售量x与利润y的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(参考公式: ![]() =
= 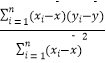 )=
)= 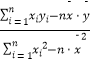 ,
, ![]() .
.
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程 ![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)满足对于任意实数a,b,c,都有f(a),f(b),f(c)为某三角形的三边长,则成f(x)为“可构造三角形函数”,已知f(x)= ![]() 是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
A.[﹣1,0]
B.(﹣∞,0]
C.[﹣2,﹣1]
D.[﹣2,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意实数x,y均有f(x)=f( ![]() )+f(
)+f( ![]() ).当x>0时,f(x)>0
).当x>0时,f(x)>0
(1)判断函数f(x)在R上的单调性并证明;
(2)设函数g(x)与函数f(x)的奇偶性相同,当x≥0时,g(x)=|x﹣m|﹣m(m>0),若对任意x∈R,不等式g(x﹣1)≤g(x)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
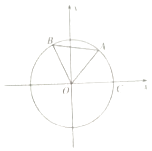
【题目】如图,点A,B是单位圆O上的两点,A,B点分别在第一,而象限,点C是圆O与x轴正半轴的交点,若∠COA=60°,∠AOB=α,点B的坐标为(﹣ ![]() ,
, ![]() ).
). 
(1)求sinα的值;
(2)已知动点P沿圆弧从C点到A点匀速运动需要2秒钟,求动点P从A点开始逆时针方向作圆周运动时,点P的纵坐标y关于时间t(秒)的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com