
分析 ①根据正态分布曲线的对称性可判定;
②根据对数的运算性质和运算法则结合非线性回归方程的求法进行判断,
③根据逆否命题的定义以及命题的等价性进行判断,
④根据不等式和函数之间的关系,利用二次函数的图象和性质即可得到结论.
解答 解:对于①,∵ξ服从正态分布N(1,σ2)(σ>0).∴正态分布曲线关于直线x=1对称,
∴若ξ在(0,1)内取值的概率为0.35,则ξ在(0,2)内取值的概率为0.7,正确;
对于②,以模型y=cekx去拟合一组数据时,设z=lny,则z=lnc+kx,
其变换后得到线性回归方程z=0.3x+4,即lnc=4,则c=e4,故正确;
对于③,若函数f(x)=ex-mx在(0,+∞)上是增函数,
则f′(x)=ex-m≥在(0,+∞)上恒成立,则m≤0”,
∴原命题为假命题,故其逆否命题是假命题,故错;
对于④,设f(x)=ax2-(a+b-1)x+b,
则f(0)=b>0,f(1)=a-(a+b-1)+b=1>0,∴要使?x>1恒成立,
则对称轴x=$\frac{a+b-1}{2a}≤1$,即a+b-1≤2a,即a≥b-1,
即不等式ax2-(a+b-1)x+b>0对?x>1恒成立的充要条件是a≥b-1.故正确,
故答案为:①②④
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较强,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{{\sqrt{2e}}}{2e}+1)$ | B. | $(1,\frac{1}{e}+1)$ | C. | $(0,\frac{1}{2e}+1)$ | D. | $(\frac{1}{e},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
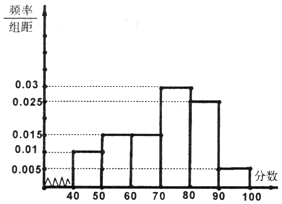 某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
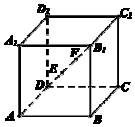 如图,在正方体ABCD-A1B1C1D1中,AB=3$\sqrt{3}$,点E,F在线段DB1上,且DE=EF=FB1,点M是正方体表面上的一动点,点P,Q是空间两动点,若$\frac{|PE|}{|PF|}$=$\frac{|QE|}{|QF|}$=2且|PQ|=4,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值为-$\frac{8}{3}$.
如图,在正方体ABCD-A1B1C1D1中,AB=3$\sqrt{3}$,点E,F在线段DB1上,且DE=EF=FB1,点M是正方体表面上的一动点,点P,Q是空间两动点,若$\frac{|PE|}{|PF|}$=$\frac{|QE|}{|QF|}$=2且|PQ|=4,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值为-$\frac{8}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com