
����Ŀ��ij���г��ĸ��������������������ˮƽ��ˮ�������������±���2011��2015���ͳ�����ݣ�
��� | 2011 | 2012 | 2013 | 2014 | 2015 |
����������ˮ������֣� | 236 | 246 | 257 | 276 | 286 |
��1���������������������������ˮ�������֮��Ļع�ֱ�߷���y=bx+a��
��2�����ݸĸ﷽����Ԥ����2020��׳��ĸ��������ʱ������������ˮ���������ȶ���Ԥ�Ƹó���2023��ľ���������ˮ����
�ο���ʽ��  ��
��
���𰸡�
��1���⣺ ![]() =2013��
=2013�� ![]() =
= ![]() =260.2��
=260.2��
![]() =����2��������24.2��+����1��������14.2��+0+1��15.8+2��25.8=130��
=����2��������24.2��+����1��������14.2��+0+1��15.8+2��25.8=130��
![]() =4+1+0+1+4=10��
=4+1+0+1+4=10��
��b= ![]() =13��
=13��
��ع鷽��Ϊy��260.2=13��x��2013������y=13��x��2013��+260.2��
��2���⣺��x=2020ʱ��y=13��2020��2013��+260.2=351.2����֣���
�𣺸ó���2023��ľ���������ˮ��Ԥ��Ϊ351.2��֣�
����������1�����ݻع�ϵ����ʽ����ع�ϵ�����ó��ع鷽�̣���2�����ڵ�2020����ˮ�������ȶ�����2023�����ˮ��Լ����2020�����ˮ������x=2020����ع鷽�������ˮ���Ĺ���ֵ��


 �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ,����
,����![]() �ĵ����ݼ����䣻
�ĵ����ݼ����䣻
��2����![]() ������
������![]() ������
������![]() �ϵ����ֵ��
�ϵ����ֵ��
��3����![]() ������
������![]() �Ϻ��������
�Ϻ��������![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪������![]() �������ⳤ����ȣ���
�������ⳤ����ȣ���![]() ��
�� ![]() ��
�� ![]() ���ֱ�Ϊ
���ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ���е㣮
���е㣮
��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����֤�� ![]() ƽ��
ƽ��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��= ![]() ΪR�ĵ�����������ʵ��a��ȡֵ��Χ�ǣ� ��
ΪR�ĵ�����������ʵ��a��ȡֵ��Χ�ǣ� ��
A.��0��+�ޣ�
B.[��1��0��
C.����2��0��
D.�����ޣ���2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxoy�У�����M����F��1��0���ľ���������ֱ��x=2�ľ���֮��Ϊ ![]() ��
��
��1����M�Ĺ켣E�ķ��̣�
��2����ֱ��y=kx+m��m��0��������E����A��B���㣬��x�ᡢy��ֱ���C��D���㣨��C��D��A��B֮���ͬʱ��A��B֮�⣩���ʣ��Ƿ���ڶ�ֵk��������������������ʵ��m�����С�OAC��������OBD�������ȣ������ڣ���k��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ����
����![]() �ĵ������䣻
�ĵ������䣻
��2����![]() ������
������![]() ��������������ʵ��
��������������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У�
�У� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() Ϊ
Ϊ![]() ���е�.
���е�.
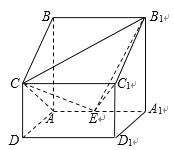
����������![]() �������
�������
�������![]() ���߶�
���߶�![]() �ϣ���ֱ��
�ϣ���ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() �����߶�
�����߶�![]() �ij��ȣ�
�ij��ȣ�
�������ж��߶�![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() �������۲�Ҫ��֤����
�������۲�Ҫ��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڴ�ҵ�����ڴ��¡������ǿ�����ڱ�������������������ȫ�������Ŀں�.ij������ҵ������Ӧ���٣������з��²�Ʒ��Ϊ�˶����з���һ����Ʒ���к������ۣ����ò�Ʒ�������ⶨ�ļ۸��������õ�һ����������![]() �����±���ʾ��
�����±���ʾ��

����֪![]() ��
��  ��.
��.
��1�����![]() ��ֵ��
��ֵ��
��2����֪����![]() ����������ع�ϵ�����Ʒ����
����������ع�ϵ�����Ʒ����![]() ������������������
������������������![]() ��Ԫ�������Իع鷽��
��Ԫ�������Իع鷽��![]() ����3����
����3����![]() ��ʾ����ȷ�����Իع鷽�̵õ�����
��ʾ����ȷ�����Իع鷽�̵õ�����![]() ��Ӧ�IJ�Ʒ�����Ĺ���ֵ.����������
��Ӧ�IJ�Ʒ�����Ĺ���ֵ.����������![]() �IJв�ľ���ֵ
�IJв�ľ���ֵ![]() ʱ������������
ʱ������������![]() ��Ϊһ���������ݡ�.�ִ�6����������ȡ2�������ȡ��2��������������1���ǡ������ݡ��ĸ���.
��Ϊһ���������ݡ�.�ִ�6����������ȡ2�������ȡ��2��������������1���ǡ������ݡ��ĸ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com