练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4—4：极坐标与参数方程

    在平面直角坐标系中，将曲线 (为参数) 上任意一点经过伸缩变换后得到曲线的图形．以坐标原点为极点，x轴的非负半轴为极轴，取相同的单位长度建立极坐标系，已知直线．

    （Ⅰ）求曲线和直线的普通方程；

    （Ⅱ）点P为曲线上的任意一点，求点P到直线的距离的最大值及取得最大值时点P的坐标．

    【答案】（1）, （2），P

    【解析】试题分析：（I）根据伸缩变换的公式代入原方程,可以得到伸缩后的曲线方程；

    （II）利用点P在椭圆上设出参数坐标,根据点到直线的距离公式求三角函数的最值,并求出取得最值时的值.

    试题解析：（I）由已知有（为参数），消去得．

    将代入直线的方程得

    曲线的方程为，直线的普通方程为.

    （II）由（I）可设点为， ．则点到直线的距离为：

    故当，即时取最大值．

    span>此时点的坐标为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点.

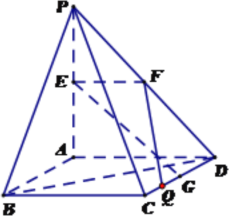
    （1）求异面直线EG与BD所成角的大小；

    （2）在线段CD上是否存在一点Q，使得点A到平面EFQ的距离恰为？若存在，求出线段CQ的长；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某超市，随机调查了100名顾客购物时使用手机支付的情况，得到如下的列联表，已知其中从使用手机支付的人群中随机抽取1人，抽到青年的概率为.

    （1）根据已知条件完成列联表，并根据此资料判断是否有的把握认为“超市购物用手机支付与年龄有关”？

    （2）现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本，设事件为“从这个样本中任选3人，这3人中至少有2人是使用手机支付的”，求事件发生的概率？

    列联表

    青年

    中老年

    合计

    使用手机支付

    60

    不使用手机支付

    28

    合计

    100

    0.001

    10.828

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，底面是边长为的菱形，，.

    （1）证明：平面；

    （2）若，求二面角 的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若曲线与直线满足：①与在某点处相切；②曲线在附近位于直线的异侧，则称曲线与直线“切过”．下列曲线和直线中，“切过”的有________．（填写相应的编号）

    ①与 ②与 ③与

    ④与 ⑤与

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来，人们对食品安全越来越重视，有机蔬菜的需求也越来越大，国家也制定出台了一系列支持有机肥产业发展的优惠政策，鼓励和引导农民增施有机肥，“藏粮于地，藏粮于技”．根据某种植基地对某种有机蔬菜产量与有机肥用量的统计，每个有机蔬菜大棚产量的增加量（百斤）与使用有机肥料（千克）之间对应数据如下表：

    使用有机肥料(千克)

    3

    4

    5

    6

    7

    8

    9

    10

    产量增加量 (百斤)

    2.1

    2.9

    3.5

    4.2

    4.8

    5.6

    6.2

    6.7

    （1）根据表中的数据，试建立关于的线性回归方程（精确到）；

    （2） 若种植基地每天早上7点将采摘的某有机蔬菜以每千克10元的价格销售到某超市，超市以每千克15元的价格卖给顾客．已知该超市每天8点开始营业，22点结束营业，超市规定：如果当天16点前该有机蔬菜没卖完，则以每千克5元的促销价格卖给顾客(根据经验，当天都能全部卖完)．该超市统计了100天该有机蔬菜在每天的16点前的销售量(单位：千克)，如表：

    每天16点前的

    销售量(单位：千克)

    100

    110

    120

    130

    140

    150

    160

    频数

    10

    20

    16

    16

    14

    14

    10

    若以100天记录的频率作为每天16点前销售量发生的概率，以该超市当天销售该有机蔬菜利润的期望值为决策依据，说明该超市选择购进该有机蔬菜110千克还是120千克，能使获得的利润更大？

    附：回归直线方程中的斜率和截距的最小二乘估计公式分别为： ，．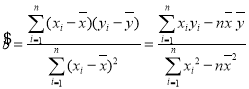

    参考数据：，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若关于的不等式的解集为，求实数的值；

    （2）设，若不等式对任意实数都成立，求实数的取值范围；

    （3）设，解关于的不等式组

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一个棱长为的正方体的表面涂上颜色，将其适当分割成棱长为的小正方体，全部放入不透明的口袋中，搅拌均匀后，从中任取一个，取出的小正方体表面仅有一个面涂有颜色的概率是（）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知如下四个命题：①在线性回归模型中，相关指数表示解释变量对于预报变量的贡献率，越接近于，表示回归效果越好；②在回归直线方程中，当解释变量每增加一个单位时，预报变量平均增加个单位；③两个变量相关性越强，则相关系数的绝对值就越接近于；④对分类变量与，对它们的随机变量的观测值来说，越小，则“与有关系”的把握程度越大．其中正确命题的序号是__________．

    查看答案和解析>>

    同步练习册答案