
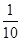 B.
B.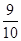 C.
C.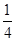 D.
D. 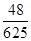
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源:不详 题型:解答题
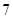 个排成一排,在下列情况下,各有多少种不同排法?
个排成一排,在下列情况下,各有多少种不同排法?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

| A.560 | B.320 | C.650 | D.360 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
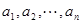 是1,2,…,
是1,2,…,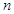 的一个排列,把排在
的一个排列,把排在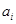 的左边且比
的左边且比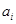 小的数的个数称为
小的数的个数称为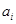 的顺序数(
的顺序数(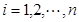 )。如:在排列
)。如:在排列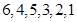 中,5的顺序数为1,3的顺序数为0。则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列种数为( )
中,5的顺序数为1,3的顺序数为0。则在1至8这八个数字构成的全排列中,同时满足8的顺序数为2,7的顺序数为3,5的顺序数为3的不同排列种数为( )| A.48 | B.96 | C.144 | D.192 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A. 85 | B. 56 | C. 49 | D. 28 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com