
【题目】已知在等差数列{an}中,a2=11,a5=5.
(1)求通项公式an;
(2)求前n项和Sn的最大值.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,可以将函数y=sin2x的图象( )
)的图象,可以将函数y=sin2x的图象( )
A.向右平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向左平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最低点为
,且图象上一个最低点为 ![]() . (Ⅰ)求f(x)的解析式;
. (Ⅰ)求f(x)的解析式;
(Ⅱ)当 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为 ![]() =(﹣k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;
=(﹣k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N; 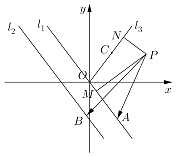
(1)若k=1,求|OM|+|ON|的值;
(2)若| ![]() |=8,求
|=8,求 ![]() 的最大值;
的最大值;
(3)若k=0,AB⊥l2 , 且Q(﹣4,﹣4),试求|PA|+|AB|+|BQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2x2+bx+c.
(1)对任意x∈[﹣1,1],f(x)的最大值与最小值之差不大于6,求b的取值范围;
(2)若f(x)=0有两个不同实根,f(f(x))无零点,求证: ![]() ﹣
﹣ ![]() >1.
>1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为 ![]() ),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( ) 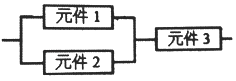
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A,ω>0,0<|φ|<π)在一个周期内的图象如图所示. 
(1)求函数f(x)的解析式;
(2)求g(x)=f(3x+ ![]() )﹣1在[﹣
)﹣1在[﹣ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理中是演绎推理的序号为( )
A.由金、银、铜、铁可导电,猜想:金属都可导电
B.猜想数列 ![]() {an}的通项公式为
{an}的通项公式为 ![]() (n∈N+)
(n∈N+)
C.半径为r圆的面积S=πr2 , 则单位圆的面积S=π
D.由平面直角坐标系中圆的方程为(x﹣a)2+(y﹣b)2=r2 , 推测空间直角坐标系中球的方程为(x﹣a)2+(y﹣b)2+(z﹣c)2=r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知圆
中,已知圆![]() :
: ![]() ,点
,点![]() ,点
,点![]() (
(![]() ),以
),以![]() 为圆心,
为圆心, ![]() 为半径作圆,交圆
为半径作圆,交圆![]() 于点
于点![]() ,且
,且![]() 的平分线交线段
的平分线交线段![]() 于点
于点![]() .
.
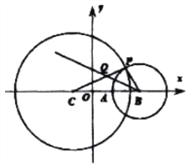
(1)当![]() 变化时,点
变化时,点![]() 始终在某圆锥曲线
始终在某圆锥曲线![]() 上运动,求曲线
上运动,求曲线![]() 的方程;
的方程;
(2)已知直线![]() 过点
过点 ![]() ,且与曲线
,且与曲线![]() 交于
交于 ![]() 两点,记
两点,记![]() 面积为
面积为![]() ,
, ![]() 面积为
面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com