
【题目】如图,四边形![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点.
上任意一点.
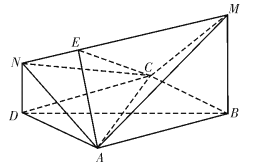
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 的最大值是
的最大值是![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)推导出AC⊥BM,AC⊥BD,从而AC⊥平面BMND,由此能证明平面EAC⊥平面BMND.
(2)由AE=CE>1,cos∠AEC=1![]() ,∠AEC∈(0,π),得到当AE最短时∠AEC最大,即AE⊥MN,CE⊥MN时∠AEC最大,∠AEC是二面角A﹣MN﹣C的平面角,大小是120°,可得AE
,∠AEC∈(0,π),得到当AE最短时∠AEC最大,即AE⊥MN,CE⊥MN时∠AEC最大,∠AEC是二面角A﹣MN﹣C的平面角,大小是120°,可得AE![]() .取MN得中点H,连接H与AC、BD的交点O,由题意知OH⊥平面ABCD,建系,利用向量法结合∠AEC=120°求得ND,利用VM﹣NAC=VM﹣EAC+VN﹣EAC能求出三棱锥M﹣NAC的体积.
.取MN得中点H,连接H与AC、BD的交点O,由题意知OH⊥平面ABCD,建系,利用向量法结合∠AEC=120°求得ND,利用VM﹣NAC=VM﹣EAC+VN﹣EAC能求出三棱锥M﹣NAC的体积.
(1)因为![]() 平面
平面![]() ,则
,则![]() .
.
又四边形![]() 是菱形,则
是菱形,则![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 在平面
在平面![]() 内,所以平面
内,所以平面![]() 平面
平面![]() .
.
(2)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() .因为
.因为![]() 平面
平面![]() ,则
,则![]() ,又
,又![]() 为
为![]() 的中点,则
的中点,则![]() ,所以
,所以![]() ,
,![]() .
.
当![]() 最短时
最短时![]() 最大,此时
最大,此时![]() ,
,![]() ,
,![]() ,
,![]() .
.
取![]() 的中点
的中点![]() ,分别以直线
,分别以直线![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
设![]() ,且a<
,且a<![]() ,
,
则点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
则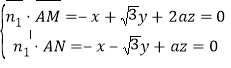 ,
,
取![]() ,则
,则![]() ,
,
同理求得平面![]() 的法向量
的法向量![]() .
.
因为![]() 是二面角
是二面角![]() 的平面角,则
的平面角,则
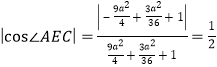 ,解得
,解得![]() 或
或![]() ,又a<
,又a<![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
则![]()
![]() .
.



 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.若![]() ,则
,则![]() ,
,![]() 的长度相等,方向相同或相反
的长度相等,方向相同或相反
B.若向量![]() 是向量
是向量![]() 的相反向量,则
的相反向量,则![]()
C.空间向量的减法满足结合律
D.在四边形![]() 中,一定有
中,一定有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若各项均不为零的数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)证明数列![]() 是等比数列,并求
是等比数列,并求![]() 的通项公式;
的通项公式;
(2)设![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立.若存在,求出正整数
恒成立.若存在,求出正整数![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要条件
”成立的充分不必要条件
B. 命题![]() ,则
,则![]()
C. 为了了解800名学生对学校某项教改试验的意见,用系统抽样的方法从中抽取一个容量为40的样本,则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-4,2)是Rt△![]() 的直角顶点,点O是坐标原点,点B在x轴上.
的直角顶点,点O是坐标原点,点B在x轴上.
(1)求直线AB的方程;
(2)求△OAB的外接圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com