
【题目】已知数列![]() 各项均为正数,
各项均为正数,![]() 为其前
为其前![]() 项的和,且
项的和,且![]() 成等差数列.
成等差数列.
(1)写出![]() 、
、![]() 、
、![]() 的值,并猜想数列
的值,并猜想数列![]() 的通项公式
的通项公式![]() ;
;
(2)证明(1)中的猜想;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.若对于任意
项和.若对于任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】某公司生产一种新产品,从产品中抽取100件作为样本,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图.
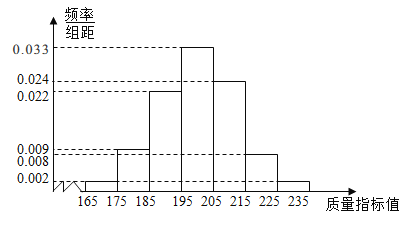
(1)用每组区间的中点值代表该组数据,估算这批产品的样本平均数![]() 和样本方差的
和样本方差的![]() ;
;
(2)从指标值落在![]() 的产品中随机抽取2件做进一步检测,设抽取的产品的指标在
的产品中随机抽取2件做进一步检测,设抽取的产品的指标在![]() 的件数为
的件数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由频率分布直方图可以认为,这种产品的质量指标值服从正态分布![]() ,
,![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,若产品质量指标值大于236.6,则产品不合格,该厂生产10万件该产品,求这批产品不合格的件数.
,若产品质量指标值大于236.6,则产品不合格,该厂生产10万件该产品,求这批产品不合格的件数.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD的中点.现分别沿BE,EC将△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,连接AD,如图2.
,E为AD的中点.现分别沿BE,EC将△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,连接AD,如图2.
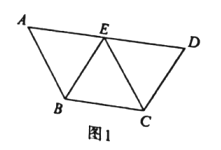
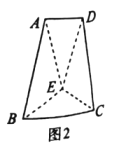
(1)若在平面BCE内存在点G,使得GD∥平面ABE,请问点G的轨迹是什么图形?并说明理由.
(2)求平面AED与平面BCE所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a R, a0,函数 f (x) eax1 ax ,其中常数e ![]() .
.
(1)求 f (x) 的最小值;
(2)当a ≥1时,求证:对任意 x0 ,都有 xf (x) ≥ 2ln x 1 ax2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场为了提高某品种水稻的产量,进行良种优选,在同一试验田中分两块种植了甲乙两种水稻.为了比较甲乙两种水稻的产量,现从甲乙两种水稻中各随机选取20株成熟水稻.根据每株水稻颗粒的重量(单位:克)绘制了如下茎叶图:
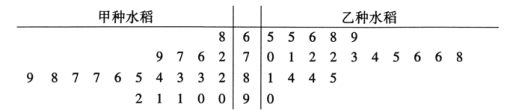
(1)根据茎叶图判断哪种水稻的产量更高?并说明理由;
(2)求40株水稻颗粒重量的中位数![]() ,并将重量超过
,并将重量超过![]() 和不超过
和不超过![]() 的水稻株数填入下面的列联表:
的水稻株数填入下面的列联表:
超过 | 不超过 | |
甲种水稻 | ||
乙种水稻 |
(3)根据(2)中的列联表,能否有![]() 的把握认为两种水稻的产量有差异?附:
的把握认为两种水稻的产量有差异?附: ;
;
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com