
分析 根据提示,分0<x<1,x=1,x>1三种情况求出数列极限$\underset{lim}{n→∞}\frac{1}{1+{x}^{n}}$,从而得出f(x)=$\left\{\begin{array}{l}{1}&{0<x<1}\\{\frac{1}{2}}&{x=1}\\{0}&{x>1}\end{array}\right.$,然后便可求出f(x)在x=1处的左右极限,从而可判断出x=1是f(x)的跳跃间断点.
解答 解:$f(x)=\left\{\begin{array}{l}{1}&{0<x<1}\\{\frac{1}{2}}&{x=1}\\{0}&{x>1}\end{array}\right.$;
∴$\underset{lim}{x→{1}^{+}}f(x)=0,\underset{lim}{x→{1}^{-}}f(x)=1$;
∴f(x)在x=1处的左右极限存在但不相等;
∴x=1是f(x)的跳跃间断点.
点评 考查数列极限和函数极限的概念和求法,函数间断点的概念及类型.


科目:高中数学 来源: 题型:解答题
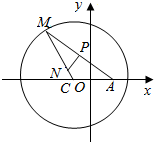 如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.
如图所示,已知圆(x+3)2+y2=100,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$,$\overrightarrow{NP}$•$\overrightarrow{AM}$=0,点N的轨迹为曲线E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑PABC中,PA⊥平面ABC,AB⊥BC,且AP=AC=1,过A点分别作AE⊥PB于E、AF⊥PC于F,连接EF当△AEF的面积最大时,tan∠BPC的值是( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{18}{5},\frac{9}{10},-\frac{1}{2}$ | B. | $-\frac{18}{5},\frac{9}{10},-\frac{1}{2}$ | C. | $\frac{18}{5},-\frac{9}{10},-\frac{1}{2}$ | D. | $-\frac{18}{5},-\frac{9}{10},\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com