Question

在四边形ABCD中,AB=CD,BC=AD(如图).求证:ABCD为平行四边形.写出三段论形式的演绎推理.

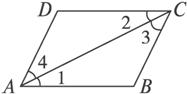
分析：原题可用符号表示为(AB=CD)且(BC=AD)ABCD.

    用演绎推理来证明论题的方法,也就是从包含在论据中的一般原理推出包含在此题中的个别特殊事实.

    为了证明这个命题为真,我们只需在假设前提(AB=CD且BC=AD)为真的情况下,以已知公理、已知定义、已知定理为依据,根据推理规则,导出结论ABCD为真.

Answer 1

证明：(1)连结AC,(公理)

(2)(AB=CD)且(BC=AD),(已知)

AC=AC,(公理)

(AB=CD)且(BC=DA)且(CA=AC).

(3)平面几何中的边边边定理是:有三边对应相等的两个三角形全等.这一定理相当于:

对于任意两个三角形,如果它们的三边对应相等,则这两个三角形全等.(大前提)

如果△ABC和△CDA的三边对应相等.(小前提)

则这两个三角形全等.(结论)

符号表示:

(AB=CD)且(BC=DA)且(CA=AC)△ABC≌△CDA.

(4)由全等形的定义,可知全等三角形的对应角相等.这一性质相当于:

对于任意两个三角形,如果它们全等,则它们对应角相等.(大前提)

如果△ABC和△CDA全等,(小前提)

则它们的对应角相等.(结论)

用符号表示,就是

△ABC≌△CDA(∠1=∠2)且(∠3=∠4)且(∠B=∠D).

(5)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.(平行线判定定理)(大前提)

直线AB、DC被直线AC所截,若内错角∠1=∠2,

∠1=∠2.(小前提)(已证)

AB∥DC,BC∥AD.

(AB∥DC)且(BC∥AD).(结论)(同理)

(6)如果四边形的两组对边分别平行,那么这个四边形是平行四边形.(平行四边形定义)(大前提)

在四边形ABCD中,两组对边分别平行,(小前提)

四边形ABCD为平行四边形.(结论)

符号表示为AB∥DC,且AD∥BC?四边形ABCD为平行四边形.

绿色通道

    像上面这样详细地分析一个证明的步骤,对于养成严谨的推理习惯,发展抽象思维能力,是有一定的积极作用,但书写起来非常烦琐,一般可以从实际出发省略大前提或小前提,采用简略的符号化写法,比如,本例题的证明,通常可以这样给出:

证明:连结AC.

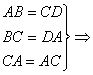△ABC≌△CDA四边形ABCD为平行四边形.