
如图,正三棱台ABC-A1B1C1中,A1B1=2,AB=4.
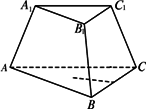
(1)若三棱台的高为3,A1B1=2,AB=4,求侧棱长及侧面与底面所成的角;
(2)若三棱台的高为h,A1B1∶AB=1∶2,过B1C1平行于相对侧棱AA1的截面把这个三棱台分成两部分,求这两部分的体积比.
|
解:(1)如图,
设正三棱台ABC-A1B1C1上、下底面中心分别为点O1、O,作O1E⊥B1C1,垂足为E,ED⊥BC,垂足为D,EF⊥OD于点F,C1G⊥CO于点G. 在Rt△CC1G中,C1G=3, CG=CO-C1O1= ∴ 由作图可知,侧面与底面所成的角就是∠EDO. 在Rt△EDF中,EF=3, DF=DO-EO1= ∴tan∠EDF= ∴∠EDF=arctan (2)设截面B1C1NM∥A1A,则B1M∥A1A∥C1N,几何体A1B1C1-AMN为三棱柱.再设三棱台的上、下底面积分别为S1、S2.
∵△A1B1C1∽△ABC,且A1B1∶AB=1∶2, ∴S1∶S2=1∶4,即S2=4S1. ∴V三棱台= V三棱柱=S1h. ∴另一部分多面体的体积V=V三棱台-V三棱柱= ∴V三棱柱∶V=3∶4. |


科目:高中数学 来源:设计必修二数学苏教版 苏教版 题型:044
如图,正三棱台ABC-A1B1C1中,若三棱台的高为h,A1B1∶AB=1∶2,过B1C1平行于相对侧棱AA1的截面把这个三棱台分成两部分,求这两部分的体积比.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟数学试卷(五)(解析版) 题型:解答题
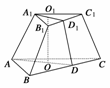
(理科)如图分别是正三棱台ABC-A1B1C1的直观图和正视图,O,O1分别是上下底面的中心,E是BC中点.

(1)求正三棱台ABC-A1B1C1的体积;
(2)求平面EA1B1与平面A1B1C1的夹角的余弦;
(3) 若P是棱A1C1上一点,求CP+PB1的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,正三棱台ABC-A1B1C1中,已知AB=10,棱台一个侧面梯形的面积为![]() ,O1、O分别为上、下底面正三角形中心,D1D为棱台的斜高,∠D1DA=60°.求上底面的边长.
,O1、O分别为上、下底面正三角形中心,D1D为棱台的斜高,∠D1DA=60°.求上底面的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com