
【题目】直三棱柱(侧棱与底面垂直的棱柱)![]() 中,D为
中,D为![]() 中点,F为线段
中点,F为线段![]() 的中点
的中点![]() .
.
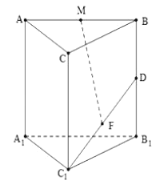
(1)若M为![]() 中点,求证:
中点,求证:![]() 面
面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,且点
上的动点,且点![]() 到椭圆
到椭圆![]() 焦点的距离的最小值为1.
焦点的距离的最小值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,当
两点,当![]() 时,求
时,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中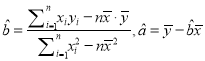 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() 是半圆
是半圆![]() 上除点
上除点![]() 外的一个动点,
外的一个动点,![]() 垂直于
垂直于![]() 所在的平面,垂足为
所在的平面,垂足为![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)当![]() 为半圆弧的中点时,求二面角
为半圆弧的中点时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,其中
,其中![]() 为常数;
为常数;
(1)若![]() ,且
,且![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,函数
,函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,在
,在![]() 上存在
上存在![]() 个点
个点![]()
![]() ,满足
,满足![]() ,
,![]() ,
,![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com