
【题目】在正方体![]() 中,下列几种说法不正确的是
中,下列几种说法不正确的是![]()
![]()
A. ![]() B. B1C与BD所成的角为60°
B. B1C与BD所成的角为60°
C. 二面角![]() 的平面角为
的平面角为![]() D.
D. ![]() 与平面ABCD所成的角为
与平面ABCD所成的角为![]()
【答案】D
【解析】
在正方体中,利用线面关系逐一判断即可.
解:对于A,连接AC,则AC⊥BD,A1C1∥AC,∴A1C1⊥BD,故A正确;
对于B,∵B1C∥![]() D,即B1C与BD所成的角为∠
D,即B1C与BD所成的角为∠![]() DB,连接
DB,连接![]()
△![]() DB为等边三角形,∴B1C与BD所成的角为60°,故B正确;
DB为等边三角形,∴B1C与BD所成的角为60°,故B正确;
对于C,∵BC⊥平面A1ABB1,A1B平面A1ABB1,∴BC⊥A1B,
∵AB⊥BC,平面A1BC∩平面BCD=BC,A1B平面A1BC,AB平面BCD,
∴∠ABA1是二面角A1﹣BC﹣D的平面角,
∵△A1AB是等腰直角三角形,∴∠ABA1=45°,故C正确;
对于D,∵C1C⊥平面ABCD,AC1∩平面ABCD=A,
∴∠C1AC是AC1与平面ABCD所成的角,∵AC≠C1C,∴∠C1AC≠45°,故D错误.
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】亳州某商场举行购物抽奖活动,规定每位顾客从装有编号为0,1,2,3四个相同小求的抽奖箱中,每次取出一球,记下编号后放回,连续取两次,若取出的两个小球号码相加之和等于6,则中一等奖;等于5中二等奖;等于4或3中三等奖.
(1)求中三等奖的概率;
(2)求不中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位有甲、乙、丙三个部门,从员工中抽取7人,进行睡眠时间的调查.若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(1)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(2)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①在线性回归模型中,相关指数![]() 越接近于1,表示回归效果越好;
越接近于1,表示回归效果越好;
②两个变量相关性越强,则相关系数r就越接近于1;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位;
平均减少0.5个单位;
④两个模型中残差平方和越小的模型拟合的效果越好.
⑤回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
⑥若![]() 的观测值满足
的观测值满足![]() ≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
⑦从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误. 其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上分布着2002 个点,现将它们任意地染成白色或黑色,如果从某一点开始,依任一方向绕圆周运动到任一点,所经过的(包括该点本身)白点总数恒大于黑点总数,则称该点为好点.为确保圆周上至少有一个好点,试求所染黑点数目的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年级100名学生期中考试数学成绩(单位:分)的频率分布直方图如图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
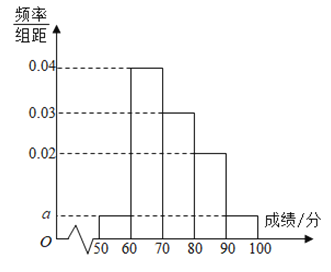
(1)求图中a的值,并根据频率分布直方图估计这100名学生数学成绩的平均分;
(2)从[70,80)和[80,90)分数段内采用分层抽样的方法抽取5名学生,求在这两个分数段各抽取的人数;
(3)现从第(2)问中抽取的5名同学中任选2名参加某项公益活动,求选出的两名同学均来自[70,80)分数段内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取![]() 人做调查,得到
人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在![]() 个人中随机抽取
个人中随机抽取![]() 人,抽到喜欢游泳的学生的概率为
人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有![]() 的把握认为喜欢游泳与性别有关?并说明你的理由.
的把握认为喜欢游泳与性别有关?并说明你的理由.
附: (其中
(其中![]() )和临界值表:
)和临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.45 | 0.708 | 1.32 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com