
【题目】如图,在直三棱柱![]() 中,底面△
中,底面△![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() 为侧棱
为侧棱![]() 的中点.
的中点.
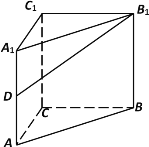
(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据等腰直角三角形的性质得到![]() ,根据直棱柱的几何性质证得
,根据直棱柱的几何性质证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(2)首先通过平移作出异面直线![]() 与
与![]() 所成的角(或其补角).解法一,通过解直角三角形求得异面直线
所成的角(或其补角).解法一,通过解直角三角形求得异面直线![]() 与
与![]() 所成的角的正切值,由此求得异面直线
所成的角的正切值,由此求得异面直线![]() 与
与![]() 所成的角的大小.解法二,利用余弦定理解三角形,求得异面直线
所成的角的大小.解法二,利用余弦定理解三角形,求得异面直线![]() 与
与![]() 所成的角的余弦值,由此求得异面直线
所成的角的余弦值,由此求得异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
(1)因为底面△![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,所以,
,所以,![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,
所以,![]() 平面
平面![]() .
.
(2)取![]() 点
点![]() ,连结
,连结![]() 、
、![]() ,则
,则![]() ∥
∥![]()
所以,![]() 就是异面直线
就是异面直线![]() 与
与![]() 所成角(或其补角).
所成角(或其补角).
解法一:由已知,![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,所以△
,所以△![]() 是直角三角形,且
是直角三角形,且![]() ,
,
因为![]() ,
,![]() ,所以,
,所以,![]() ,
,
所以,异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
解法二:在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理得,![]()
![]() .
.
所以,异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.


科目:高中数学 来源: 题型:
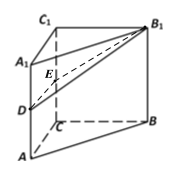
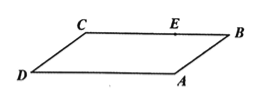
【题目】如图,有一块平行四边形绿地![]() ,经测量
,经测量![]() 百米,
百米,![]() 百米,
百米,![]() ,拟过线段
,拟过线段![]() 上一点
上一点![]() 设计一条直路
设计一条直路![]() (点
(点![]() 在四边形
在四边形![]() 的边上,不计路的宽度),
的边上,不计路的宽度),![]() 将绿地分成两部分,且右边面积是左边面积的3倍,设
将绿地分成两部分,且右边面积是左边面积的3倍,设![]() 百米,
百米,![]() 百米.
百米.
(1)当点![]() 与点
与点![]() 重合时,试确定点
重合时,试确定点![]() 的位置;
的位置;
(2)试求![]() 的值,使路
的值,使路![]() 的长度
的长度![]() 最短.
最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的前n项和Sn满足S1>1,且![]() (nN*).
(nN*).
(1)求{an}的通项公式;
(2)设数列![]() 满足
满足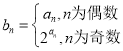 ,Tn为数列{bn}的前n项和,求Tn;
,Tn为数列{bn}的前n项和,求Tn;
(3)设![]() *(
*(![]() 为正整数),问是否存在正整数
为正整数),问是否存在正整数![]() ,使得当任意正整数n>N时恒有Cn>2015成立?若存在,请求出正整数
,使得当任意正整数n>N时恒有Cn>2015成立?若存在,请求出正整数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,![]() 为坐标原点,C、D两点的坐标为
为坐标原点,C、D两点的坐标为![]() ,曲线
,曲线![]() 上的动点P满足
上的动点P满足![]() .又曲线
.又曲线![]() 上的点A、B满足
上的点A、B满足![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点A在第一象限,且![]() ,求点A的坐标;
,求点A的坐标;
(3)求证:原点到直线AB的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数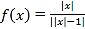 ,给出以下四个命题:(1)当
,给出以下四个命题:(1)当![]() 时,
时,![]() 单调递减且没有最值;(2)方程
单调递减且没有最值;(2)方程![]() 一定有实数解;(3)如果方程
一定有实数解;(3)如果方程![]() (
(![]() 为常数)有解,则解得个数一定是偶数;(4)
为常数)有解,则解得个数一定是偶数;(4)![]() 是偶函数且有最小值.其中假命题的序号是____________.
是偶函数且有最小值.其中假命题的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列 ![]() 的前
的前![]() 项和为
项和为![]() ,对一切
,对一切![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明);
的通项公式(不必证明);
(2)将数列![]() 依次按1项、2项、3项、4项循环地分为
依次按1项、2项、3项、4项循环地分为![]() ,
,![]() ,
,![]() ,
, ![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 为数列
为数列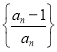 的前
的前![]() 项积,若不等式
项积,若不等式![]() 对一切
对一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() 。我们将其结论推广:椭圆
。我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用。已知,直线
,在解本题时可以直接应用。已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
(1)求![]() 的值;
的值;
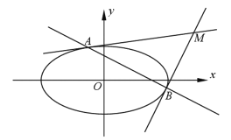
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() 。当
。当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)在(2)的条件下,经过点![]() 作直线
作直线![]() 与该椭圆
与该椭圆![]() 交于
交于![]() 、
、![]() 两点,在线段
两点,在线段![]() 上存在点
上存在点![]() ,使
,使![]() 成立,试问:点
成立,试问:点![]() 是否在直线
是否在直线![]() 上,请说明理由.
上,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,
的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)设点![]() 在椭圆
在椭圆![]() 上运动,
上运动,![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为常数
的距离为常数![]() ,求动点
,求动点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com