
【题目】如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB= ![]() AD=2,点G为AC的中点.
AD=2,点G为AC的中点. 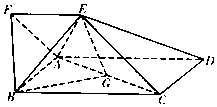
(Ⅰ)求证:平面BAE⊥平面DCE;
(Ⅱ)求三棱锥B﹣AEG的体积.
【答案】证明:(Ⅰ)∵四边形ABCD为矩形,且平面ABCD⊥平面AFED,
∴CD⊥平面AFED,∴CD⊥AE,
∵∠AED=90°,∴ED⊥AE,
又∵EO∩CD=D,∴AE⊥平面DCE,
又AE平面BAE,∴平面BAE⊥平面DCE.
(Ⅱ)作EN⊥AD,垂足为N,
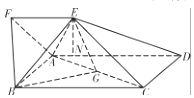
由平面ABCD⊥平面AFED,平面ABCD∩平面AFED=AD.
得EN⊥平面ABCD,即EN为三棱锥E﹣ABG的高.
∵在△AEF中,AF=FE,∠AFE=60°,∴△AEF是正三角形,AE=2,
由EF∥AD,知∠EAD=60°,∴ ![]() ,
,
∴三棱锥B﹣AEG的体积为:
![]() .
.
【解析】(Ⅰ)推导出CD⊥AE,ED⊥AE,从而AE⊥平面DCE,由此能证明平面BAE⊥平面DCE.(Ⅱ)作EN⊥AD,垂足为N,三棱锥B﹣AEG的体积为VB﹣AEG=VE﹣ABG,由此能求出结果.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() ,动直线
,动直线 ![]()
(1)若动直线l与椭圆C相交,求实数m的取值范围;
(2)当动直线l与椭圆C相交时,证明:这些直线被椭圆截得的线段的中点都在直线3x+2y=0上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0.
(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个命题: ①若直线a,b异面,b,c异面,则a,c异面;
②若直线a,b相交,b,c相交,则a,c相交;
③若a∥b,则a,b与c所成的角相等;
④若a⊥b,b⊥c,则a∥c.
其中真命题的个数为( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的所对的边分别为a,b,c,且a2+b2=ab+c2 .
(Ⅰ) 求tan(C﹣ ![]() )的值;
)的值;
(Ⅱ) 若c= ![]() ,求S△ABC的最大值.
,求S△ABC的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,表示同一集合的是( )
A.A={0,1},B={(0,1)}
B.A={2,3},B={3,2}
C.A={x|﹣1<x≤1,x∈N},B={1}
D.![]()
E.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com